Lecture 11

Julia Schedler

Announcements

Assignment 4 posted

Last time

U.S. GNP data– clearly has a trend, nonstationary

Code

library(fpp3); library(astsa)
tsplot(gnp)

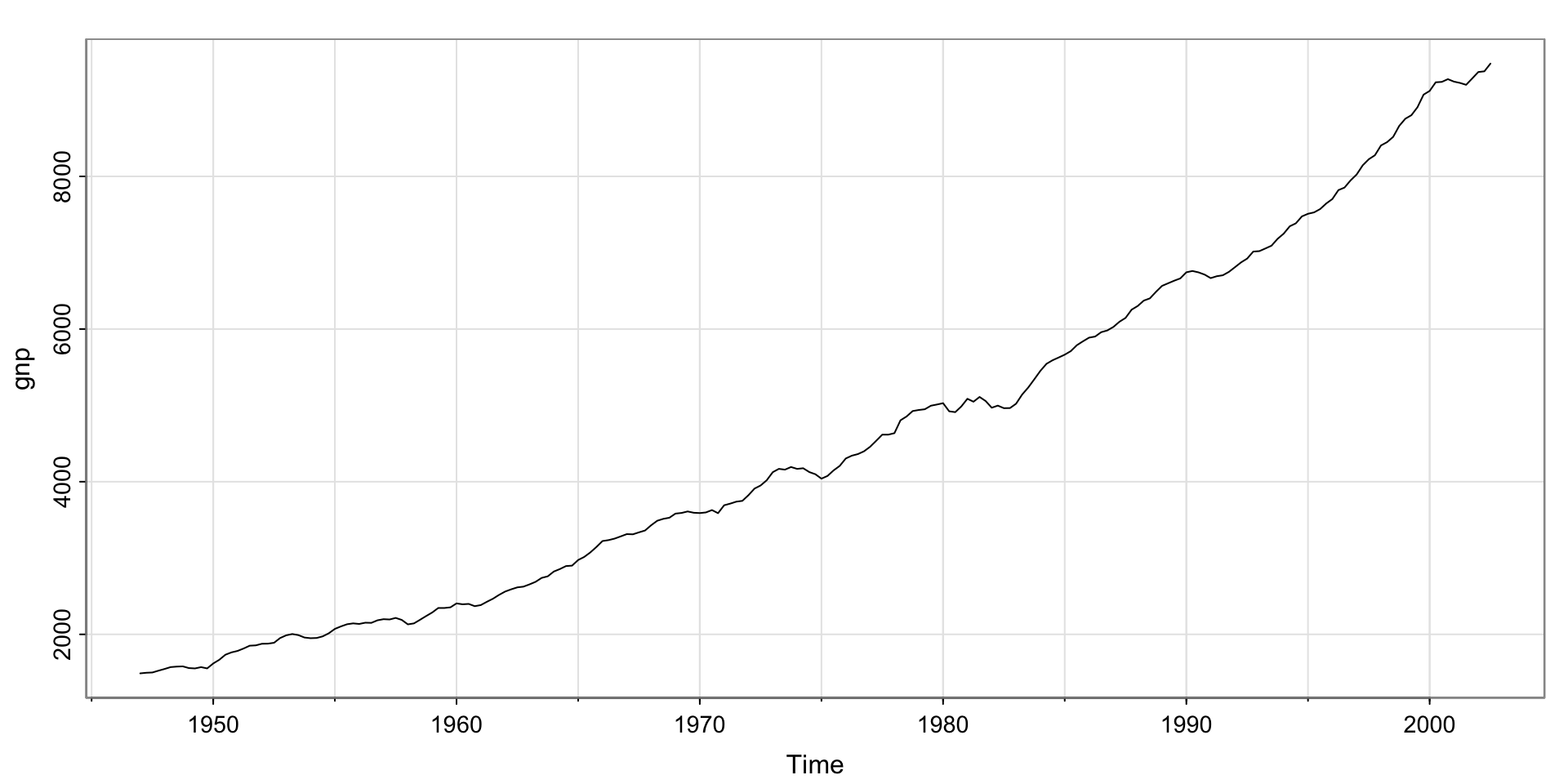
Is the trend linear?

Not exactly…

Code

tsplot(gnp)
abline(lm(gnp~time(gnp)), col = "blueviolet", lwd = 2)

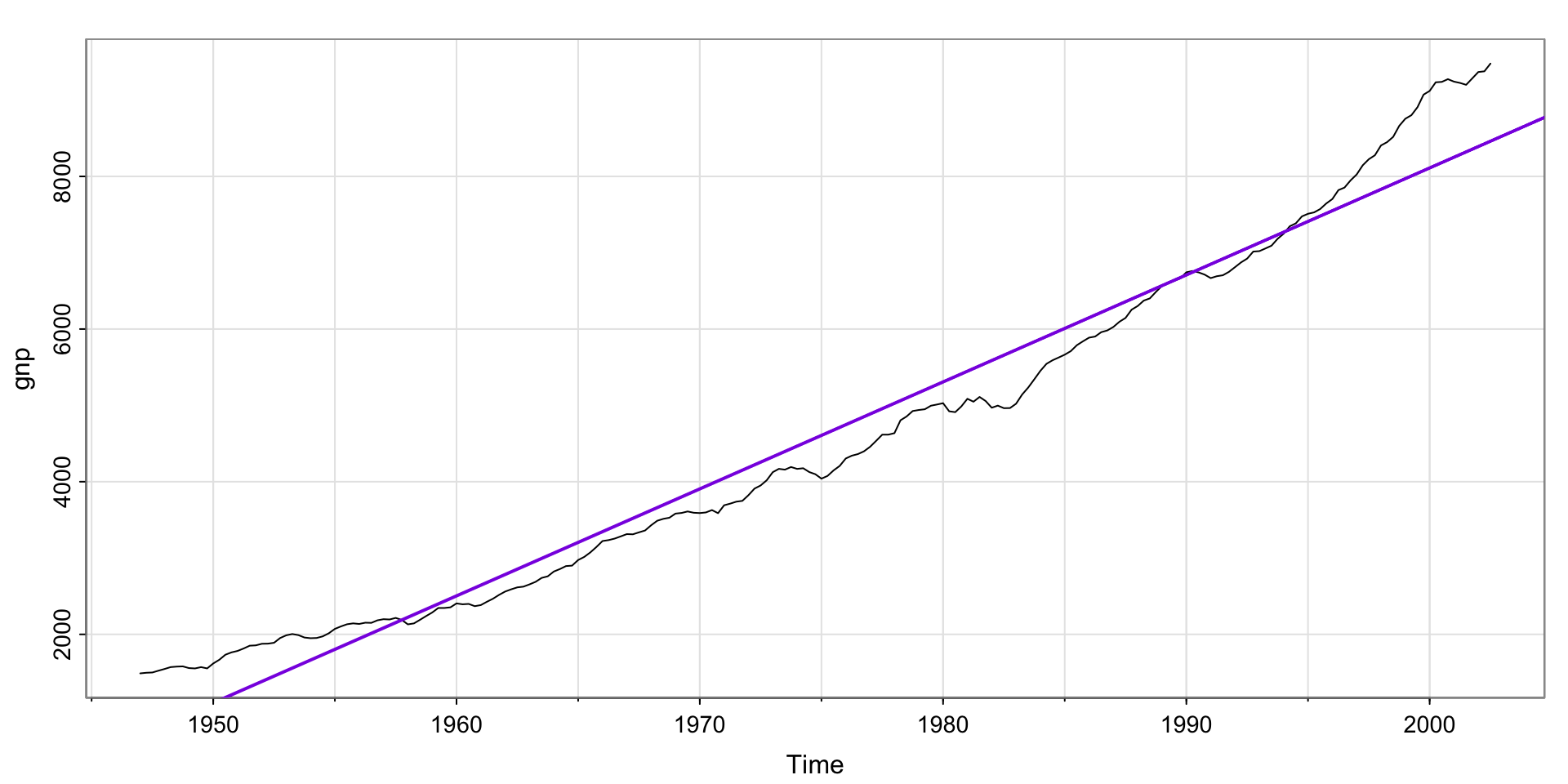
Try taking the log?

Much better! But, still not stationary.

Code

log_gnp <- log(gnp)
tsplot(log_gnp)
abline(lm(log_gnp~time(log_gnp)), col = "blueviolet", lwd = 2)

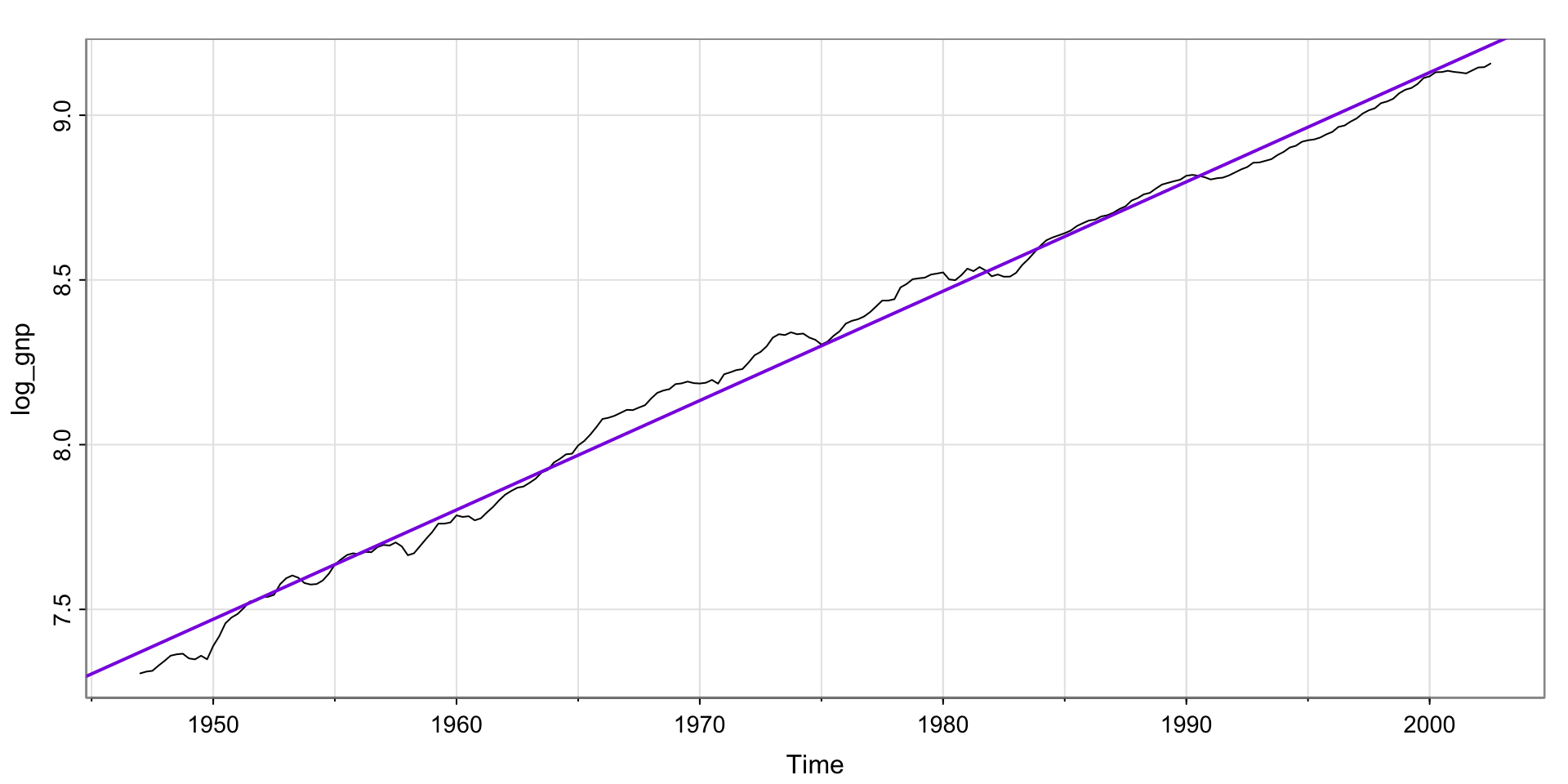
Try differencing?

Is this stationary? No? Yes? Maybe there’s a bit of a trend?

Code

tsplot(diff(log_gnp))

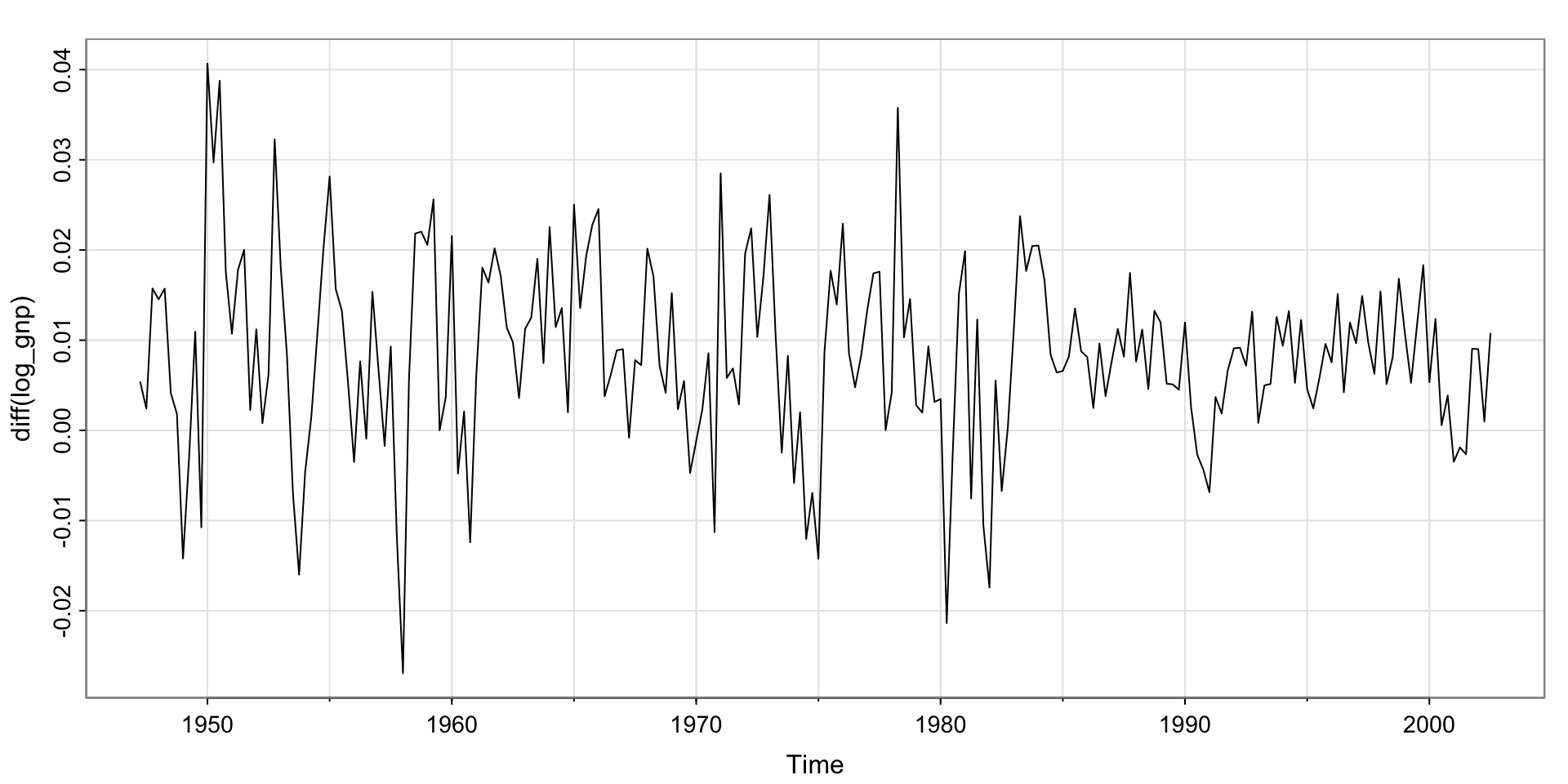
Unit root tests

Augmented Dickey-Fuller (ADF)

Null hypothesis: random walk (nonstationary)
Alternative hypothesis: stationary data

Kwiatkowski-Phillips-Schmidt-Shin (KPSS)

Null hypothesis: stationary data
Alternative hypothesis: nonstationary data

What’s a unit?

1 (one)

What’s a root of a polynomial?

Example:Find the roots of \(1 - Ax + Bx^2 = 0\)

Use the quadratic formula:

\[ x = \frac{A \pm \sqrt{A^2 - 4B }}{2B} \] A unit root would be where \(x = 1\) is a solution.

What do we care about being one?

For an AR(1),

\[ x_t = \phi x_{t-1} + w_t \]

If \(\phi = 1\), we have a random walk (nonstationary). We’d like a hypothesis test that is able to use information about plausible values of \(\phi\) so that we can see if 1 is plausible.

Wait, where’s the polynomial? (Advanced topic)

It’s the AR polynomial– the polynomial with respect to the lag operator. If the AR polynomial has a unit root, the data are nonstationary.

But since it corresponds to having \(\phi = 1\), we can derive the distribution of our estimate of \(\phi\), \(\widehat{\phi}\), and use reasonable distributional assumptions so that we can calculate a p-value. If the roots are less than or equal to 1, that’s nonstationary.

Unit root test in `R` using `features` function

Code

log_gnp |> 
  diff() |>
  as_tsibble() |> 
  features(value, unitroot_kpss)

# A tibble: 1 × 2
  kpss_stat kpss_pvalue
      <dbl>       <dbl>
1     0.141         0.1

Since the p-value is not very small, we fail to reject the null hypothesis that the data is stationary.

Activity 0

## find the number of differences needed to make the *original* data (not log transformed) stationary

In practice

Use the unitroot_ndiffs() function to figure out how many differences you need.

ndiffs_lognp <- log_gnp |> 
  as_tsibble() |> 
  features(value, unitroot_ndiffs)

ndiffs_lognp

# A tibble: 1 × 1
  ndiffs
   <int>
1      1

## note-- if we did not take the log, it says we'd need two!
gnp |> 
  as_tsibble() |> 
  features(value, unitroot_ndiffs)

# A tibble: 1 × 1
  ndiffs
   <int>
1      2

Recall the ARIMA modeling workflow

Activity 1: Manual analysis

Find the order of the ARMA(p,q) process for the log differenced GNP.
Check the residuals

Activity 1 Solutions (manual)

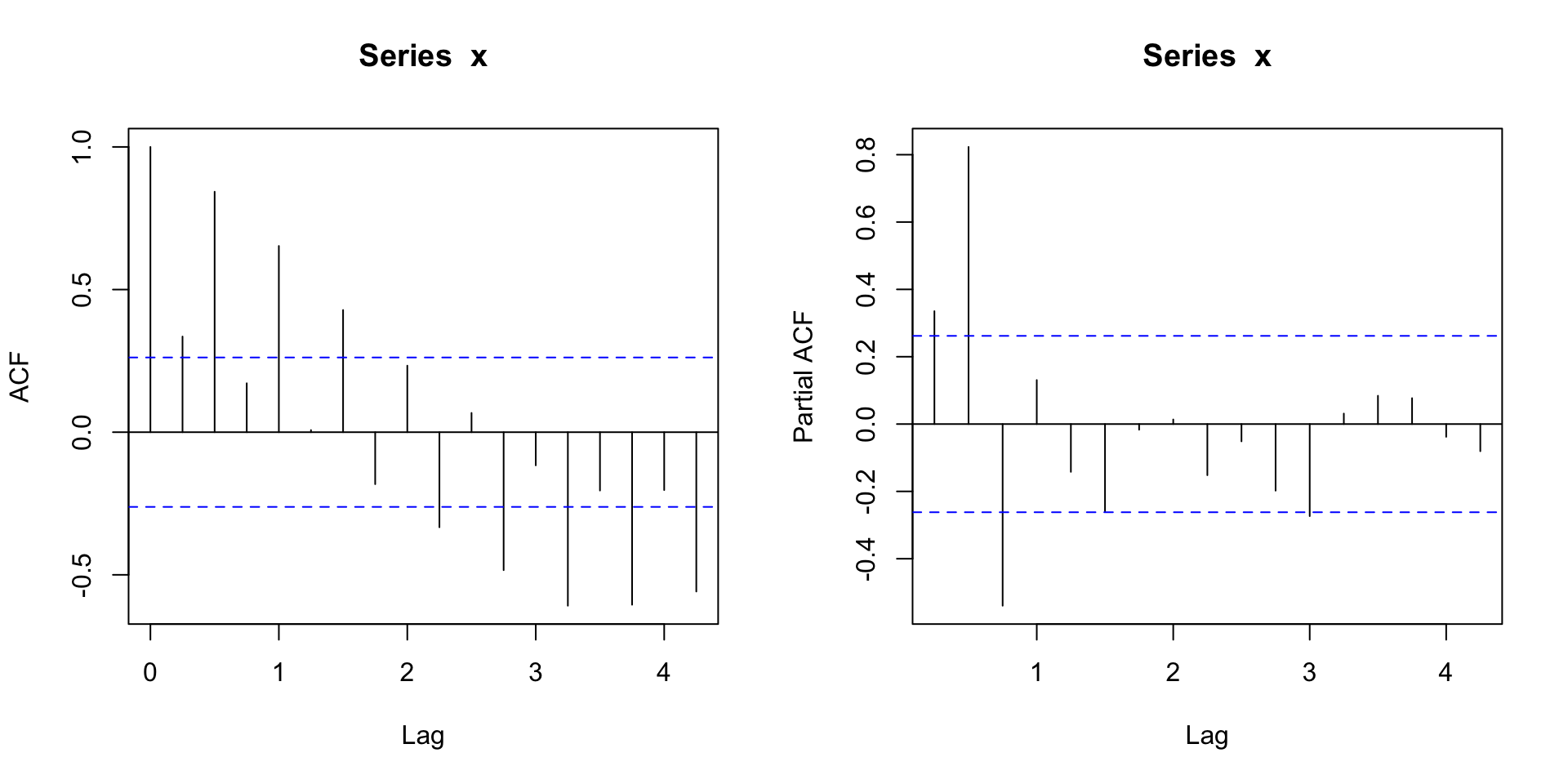
Manual: look at ACF and PACF. The ACF maybe cuts at lag 2 and the PACF appears to tail off. So maybe MA(2)?

Code

diff_log_gnp <- diff(log_gnp, differences = ndiffs_lognp$ndiffs)

par(mfrow = c(1,2))
diff_log_gnp |> 
  acf1()

 [1]  0.35  0.19 -0.01 -0.12 -0.17 -0.11 -0.09 -0.04  0.04  0.05  0.03 -0.12
[13] -0.13 -0.10 -0.11  0.05  0.07  0.10  0.06  0.07 -0.09 -0.05 -0.10 -0.05
[25]  0.00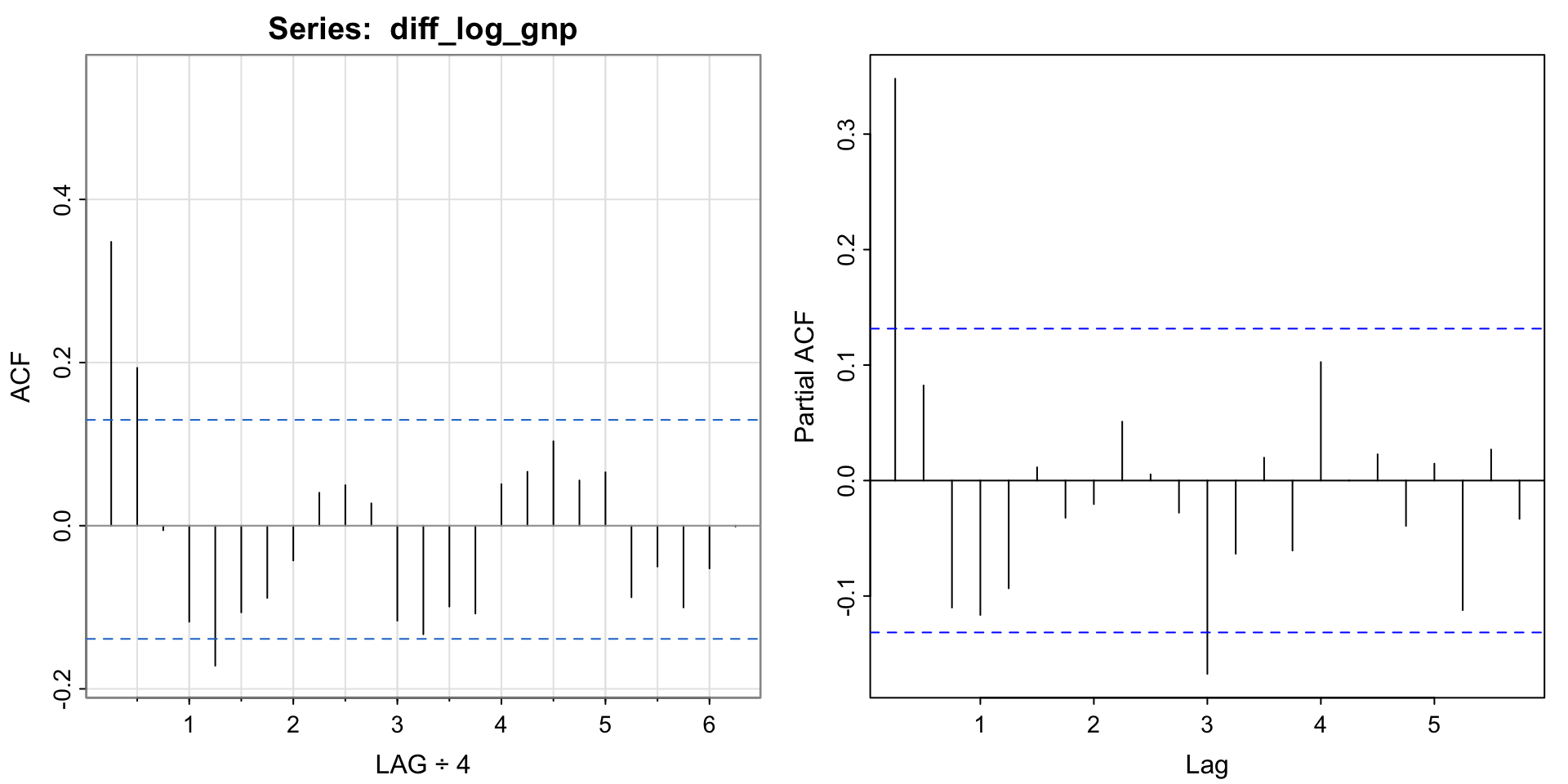

Code

diff_log_gnp |> 
  pacf()

Handy table

	AR(p)	MA(q)	ARMA(p,q)
ACF	Tails off	Cuts off after lag q	Tails off
PACF	Cuts off after lag p	Tails off	Tails off

Activity 1 Solutions (manual)

Code

diff_log_gnp |> 
  as_tsibble() |>
  model(ARIMA(value ~ pdq(0,0,2) + PDQ(0,0,0))) |> ## force nonseasonal
  report()

Series: value 
Model: ARIMA(0,0,2) w/ mean 

Coefficients:
         ma1     ma2  constant
      0.3028  0.2035    0.0083
s.e.  0.0654  0.0644    0.0010

sigma^2 estimated as 9.041e-05:  log likelihood=719.96
AIC=-1431.93   AICc=-1431.75   BIC=-1418.32

Activity 1 Solutions

Code

manual_fit <- diff_log_gnp |> 
  as_tsibble() |>
  model(ARIMA(value ~ pdq(0,0,2) + PDQ(0,0,0)))

residuals(manual_fit) |> gg_tsdisplay(plot_type = "histogram")

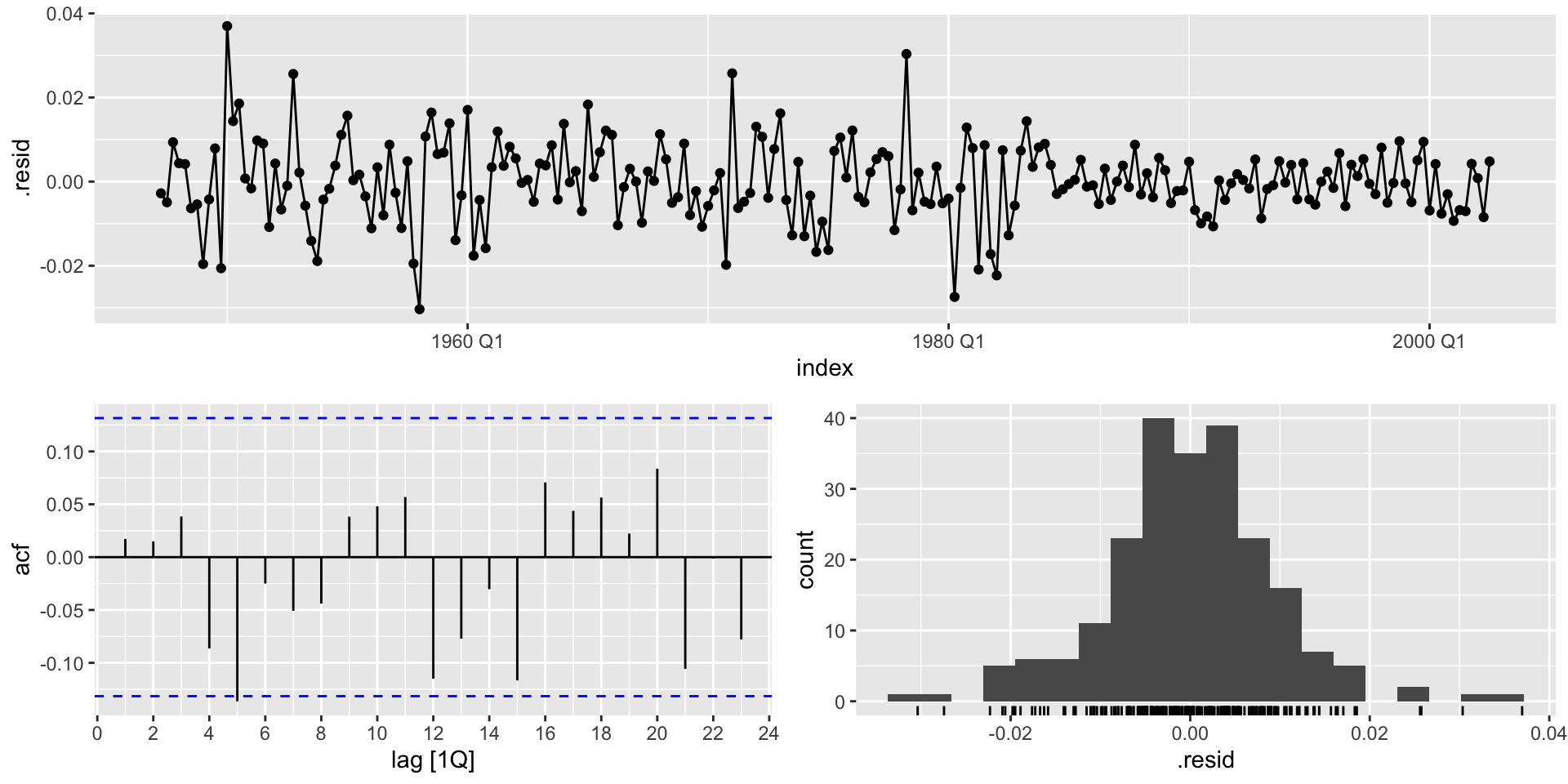
The residuals look like white noise

What about automatic?

Different answer– but, looking at the ACFS, kind of reasonable.

Code

diff_log_gnp |> 
  as_tsibble() |>
  model(ARIMA(value)) |>
  report()

Series: value 
Model: ARIMA(1,0,0) w/ mean 

Coefficients:
         ar1  constant
      0.3467    0.0054
s.e.  0.0627    0.0006

sigma^2 estimated as 9.112e-05:  log likelihood=718.61
AIC=-1431.22   AICc=-1431.11   BIC=-1421.01

Specifying \(d\) in the `ARIMA` call

Work with the non-differenced data, and specify \(d =1\) in pdq(). We get the same estimated model.

Code

ar1_fit_fable <- log_gnp |> 
  as_tsibble() |>
  model(ARIMA(value ~ pdq(1,1,0) + PDQ(0,0,0))) ## force nonseasonal
  
report(ar1_fit_fable)

Series: value 
Model: ARIMA(1,1,0) w/ drift 

Coefficients:
         ar1  constant
      0.3467    0.0054
s.e.  0.0627    0.0006

sigma^2 estimated as 9.136e-05:  log likelihood=718.61
AIC=-1431.22   AICc=-1431.11   BIC=-1421.01

Going fully automated

Allow ARIMA to choose the order of the differencing \(d\) and \(p,q\).

Based on corrected AIC, this is slightly better than our model. But this model is quite complicated!

Code

fully_auto_fit <- log_gnp |> 
  as_tsibble() |>
  model(ARIMA(value ~ PDQ(0,0,0))) |> ## force nonseasonal
  
  report(fully_auto_fit)

Series: value 
Model: ARIMA(3,1,1) w/ drift 

Coefficients:
         ar1      ar2      ar3      ma1  constant
      1.0905  -0.1251  -0.1739  -0.7881    0.0017
s.e.  0.3027   0.1529   0.0777   0.3112    0.0001

sigma^2 estimated as 8.906e-05:  log likelihood=722.89
AIC=-1433.78   AICc=-1433.39   BIC=-1413.36

Activity 2: Should we go fully automated??

Go to the ASTSA package github and click “Estimation” under 4.ARIMA
Read between the watermelon 🍉 and alien 👽
Are they using the ARIMA function? Is the function they are using different?
Explain how the code under “DON’T BELIEVE IT?? OK… HERE YOU GO” provides evidence that automatic arima functions don’t work

Using the `sarima` function for diagnostics

Code

sarima(log_gnp, p = 1, d = 1, q = 0)

initial  value -4.589567 
iter   2 value -4.654150
iter   3 value -4.654150
iter   4 value -4.654151
iter   4 value -4.654151
iter   4 value -4.654151
final  value -4.654151 
converged
initial  value -4.655919 
iter   2 value -4.655921
iter   3 value -4.655921
iter   4 value -4.655922
iter   5 value -4.655922
iter   5 value -4.655922
iter   5 value -4.655922
final  value -4.655922 
converged
<><><><><><><><><><><><><><>
 
Coefficients: 
         Estimate     SE t.value p.value
ar1        0.3467 0.0627  5.5255       0
constant   0.0083 0.0010  8.5398       0

sigma^2 estimated as 9.029576e-05 on 220 degrees of freedom 
 
AIC = -6.446939  AICc = -6.446692  BIC = -6.400957

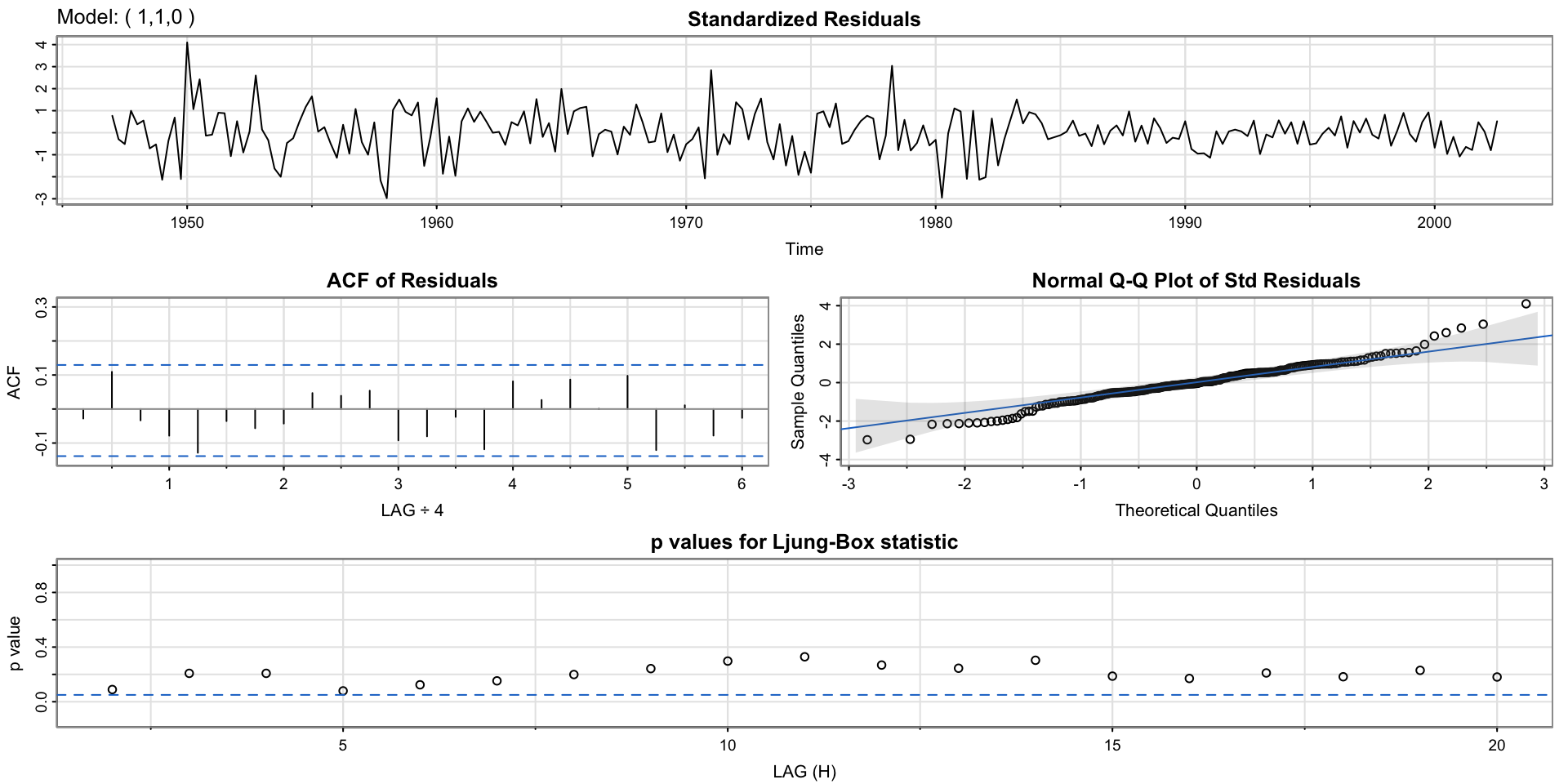
Activity 3: p-values for Ljung-Box statistic

When an R function for fitting a model gives you a diagnostic plot by default, it’s good to understand that plot– it’s probably useful!
Use whatever resources you can to figure out what that bottom plot means

Testing if the residuals are white noise

Portmanteau tests (French for suitcase or coat rack carrying several items of clothing) (do the residuals “carry information”

Null hypothesis: Residuals are generated by a white noise process.
Alternative hypothesis: Residuals are not generated by a white noise process.

Lots of options for tests, we will use Ljung-Box (default output)

Ljung-box in `fable`

Code

residuals(ar1_fit_fable) |>
features(.resid,ljung_box, lag = 10)

# A tibble: 1 × 3
  .model                                     lb_stat lb_pvalue
  <chr>                                        <dbl>     <dbl>
1 ARIMA(value ~ pdq(1, 1, 0) + PDQ(0, 0, 0))    10.7     0.382

Seasonal Arima models

Goal: define Seasonal Arima model

Want:

\[ ARIMA(p, d, q)\times(P,D,Q)_{S} \]

first part is the same as before– nonseasonal
second part is similar to before, but we interpret lags as having a seasonal period.

Pure Seasonal ARIMA

A time series \(x_t\) is said to follow a Pure Seasonal ARIMA model, with parameters \(P, D, Q\), and seasonal period \(S\) (or \(T\)), if

\(x_t\) has a seasonal component with period \(S\)
is ARIMA(P,D,Q) where we interpret the lag as a seasonal lag, i.e. lagging by \(S\)

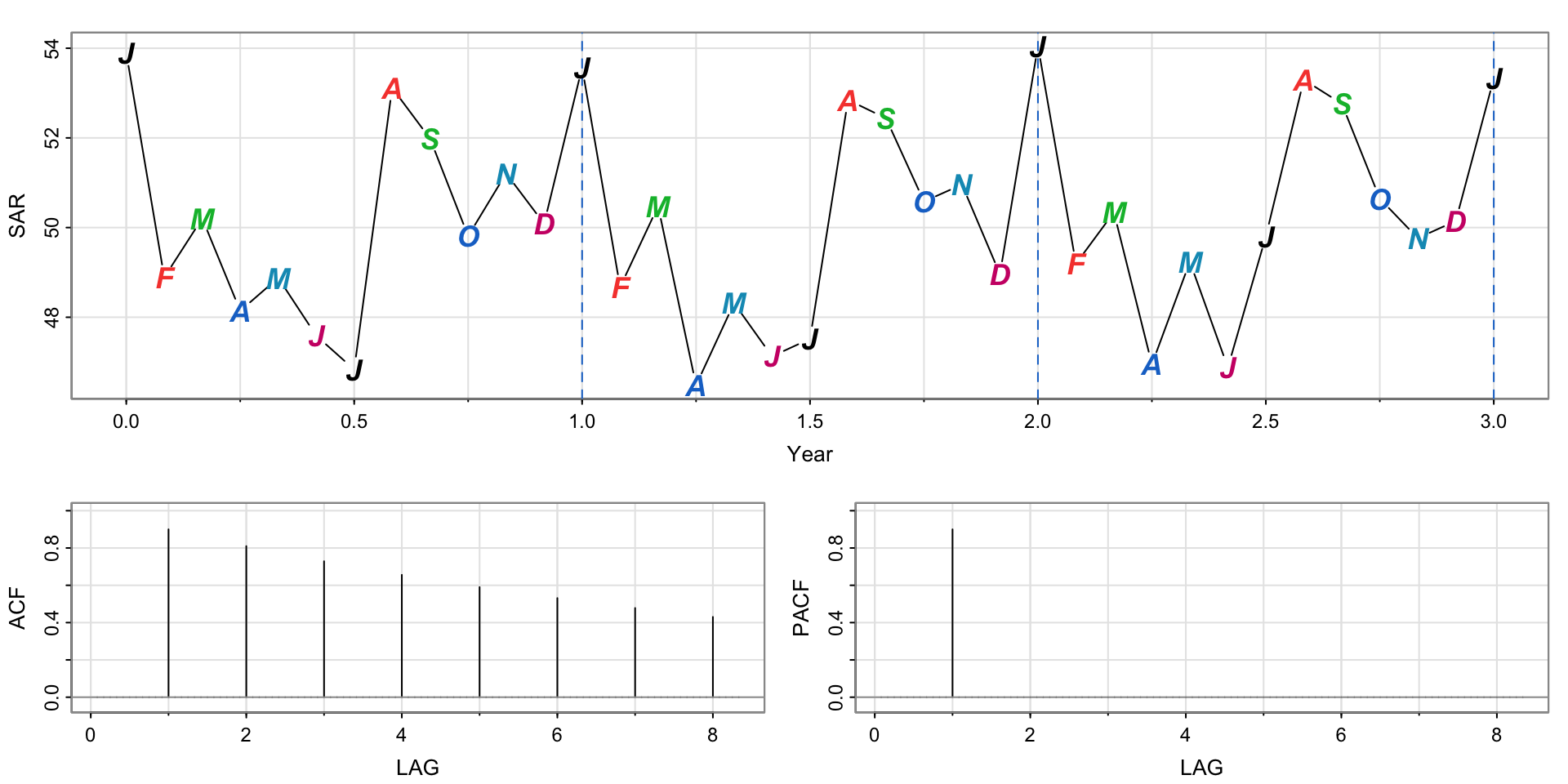
Simulating a pure seasonal AR(1) process

Notice the peaks every January– the seasonal period here is 12 (or 1 if we divide by 12).

The same “tailing off”/“cutting off” behavior is the same, but we look for seasonal spikes

Hawaiian Quarterly Occupancy

The two plots show the time series, and the extracted seasonal component.

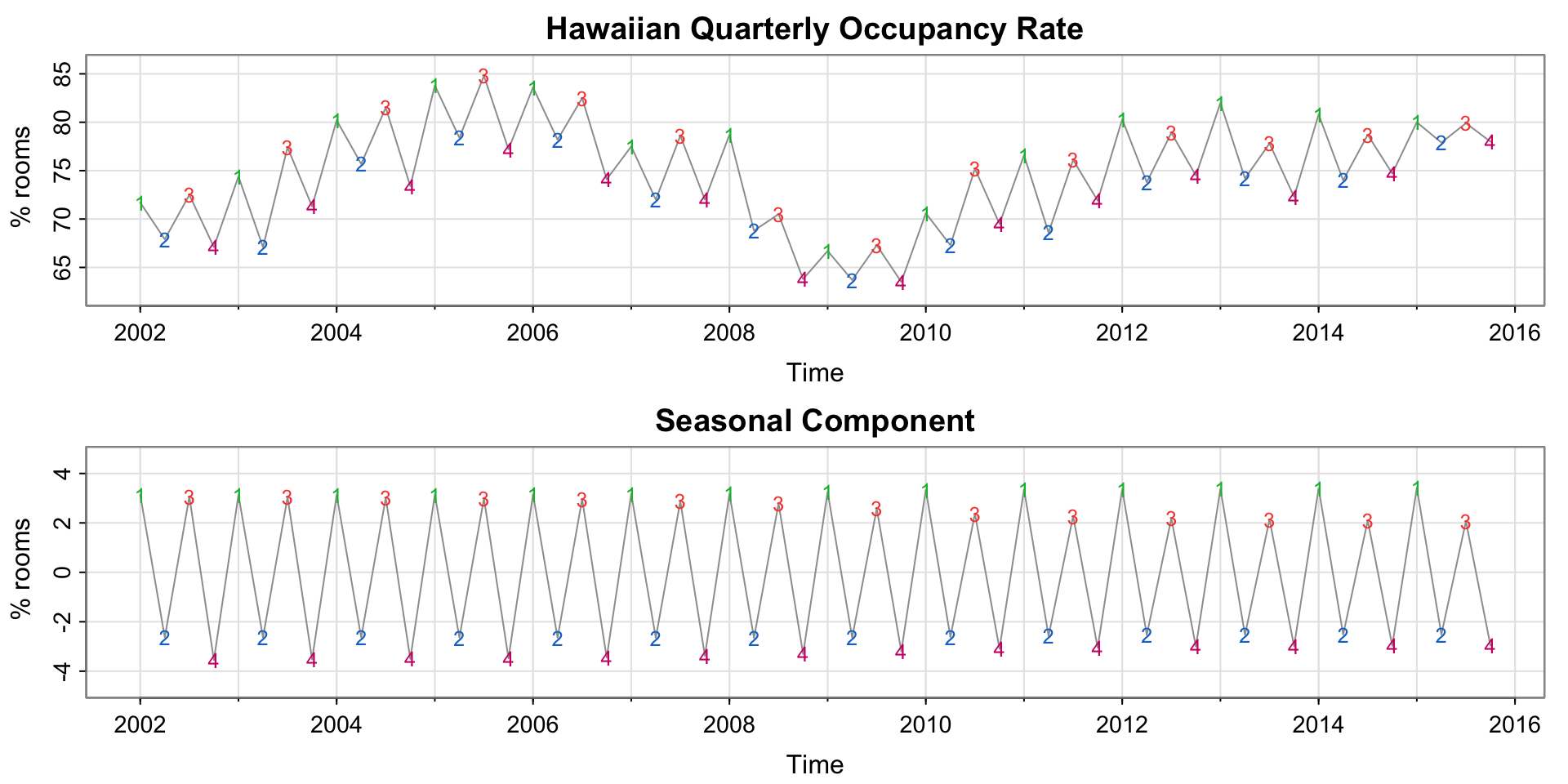
Hawaiian Quarterly Occupancy

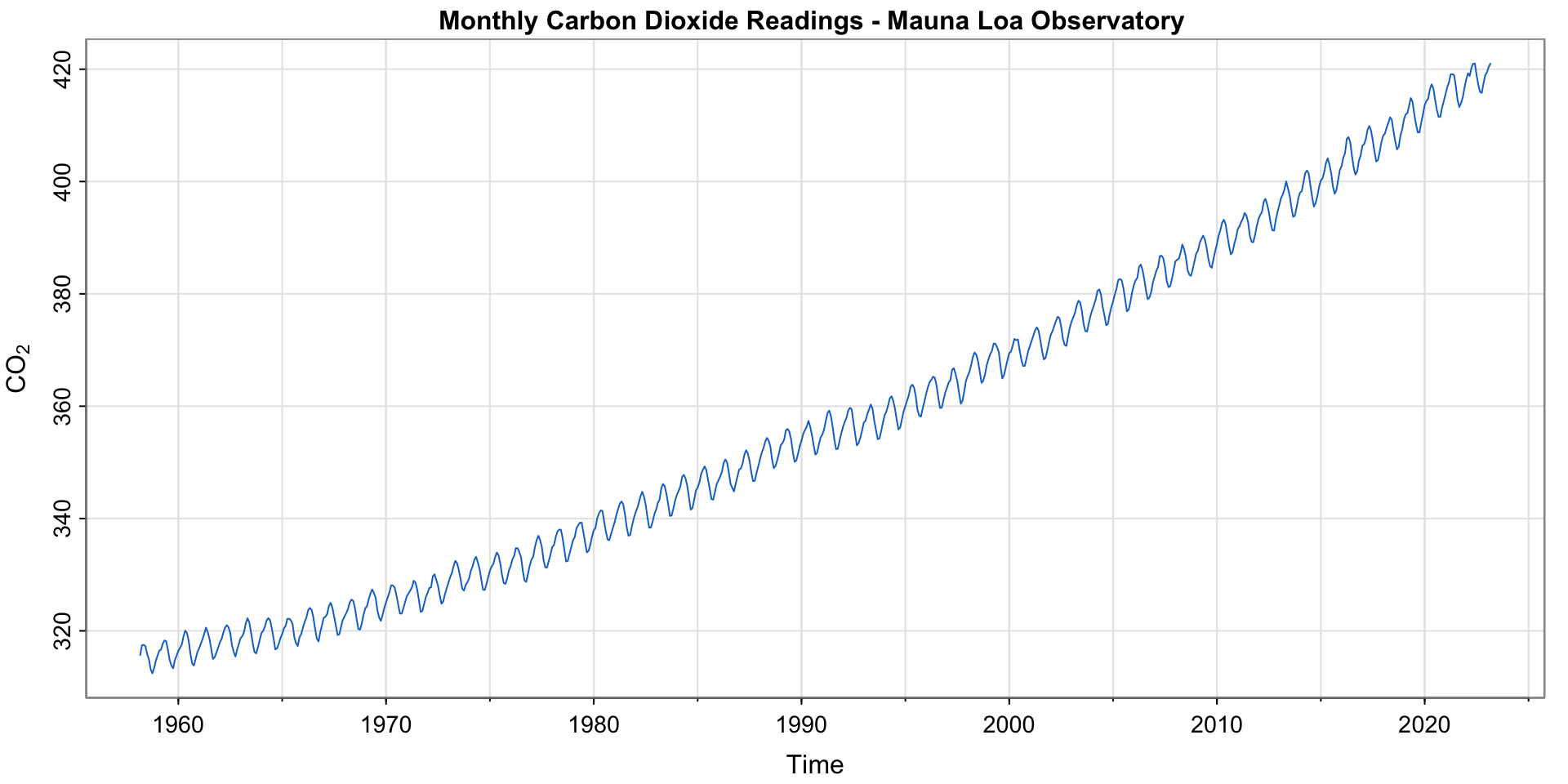
Carbon Dioxide Readings

Monthly \(CO_2\) readings at Mauna Loa Observatory

Do we see a seasonal pattern?

Code

tsplot(cardox, col=4, ylab=expression(CO[2]))
title("Monthly Carbon Dioxide Readings - Mauna Loa Observatory ", cex.main=1)

What’s the acf?

Code

acf(cardox)

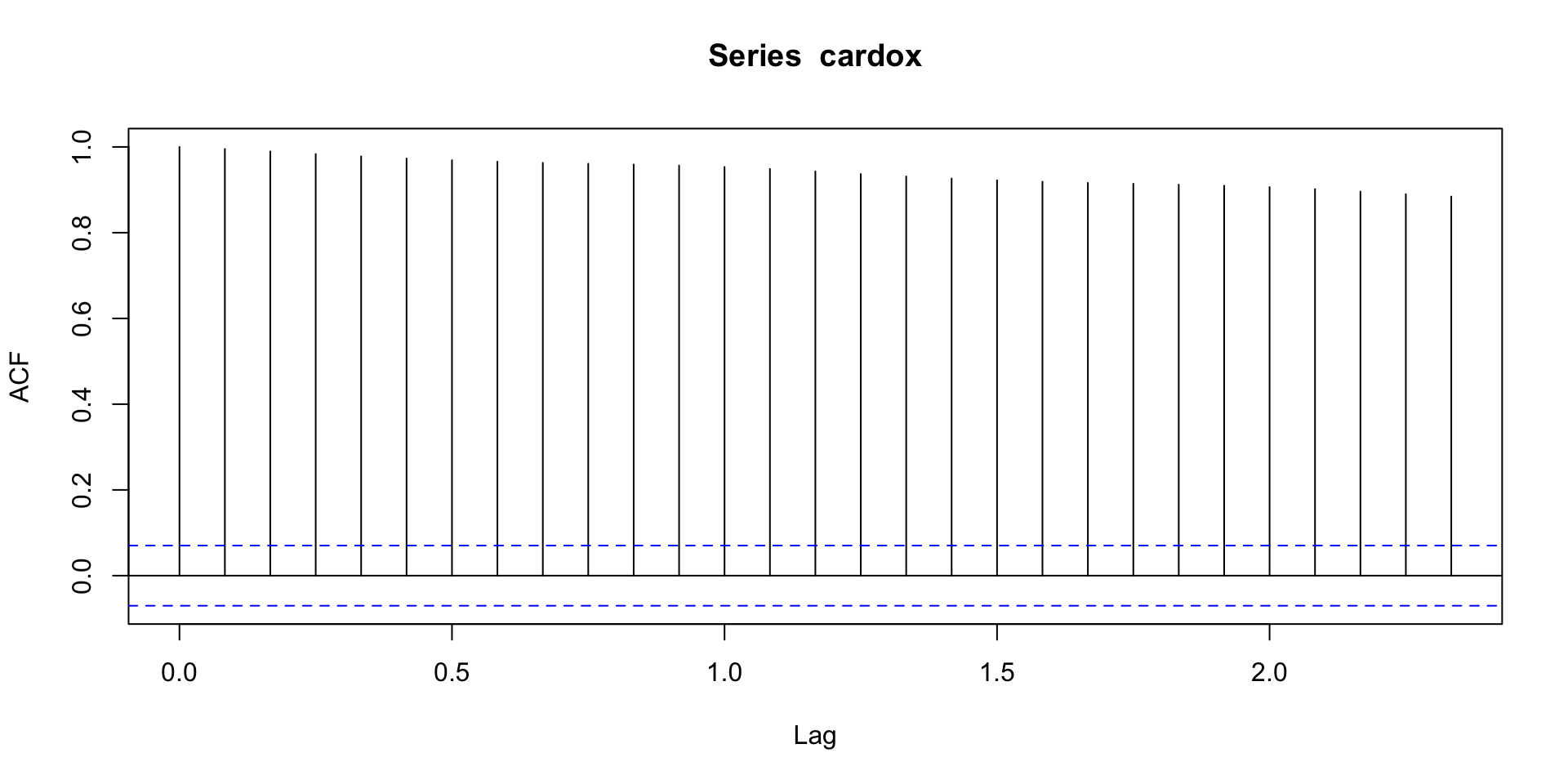
Let’s try a seasonal difference!

Code

tsplot(diff(cardox,12), col=4, 
ylab=expression(nabla[12]~CO[2]))

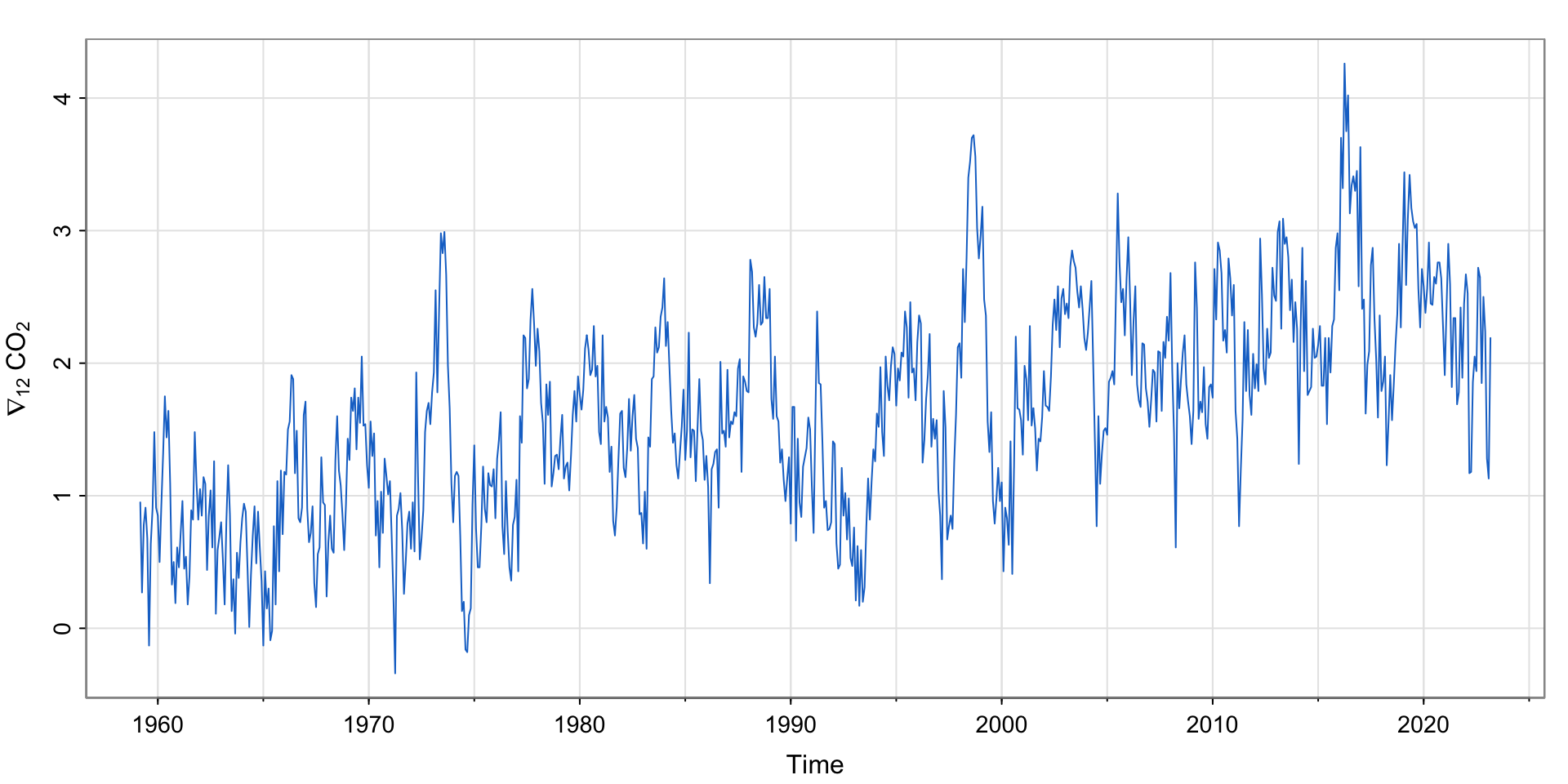
Check the acf

Still a trend..difference again?

Code

acf(diff(cardox, 12))

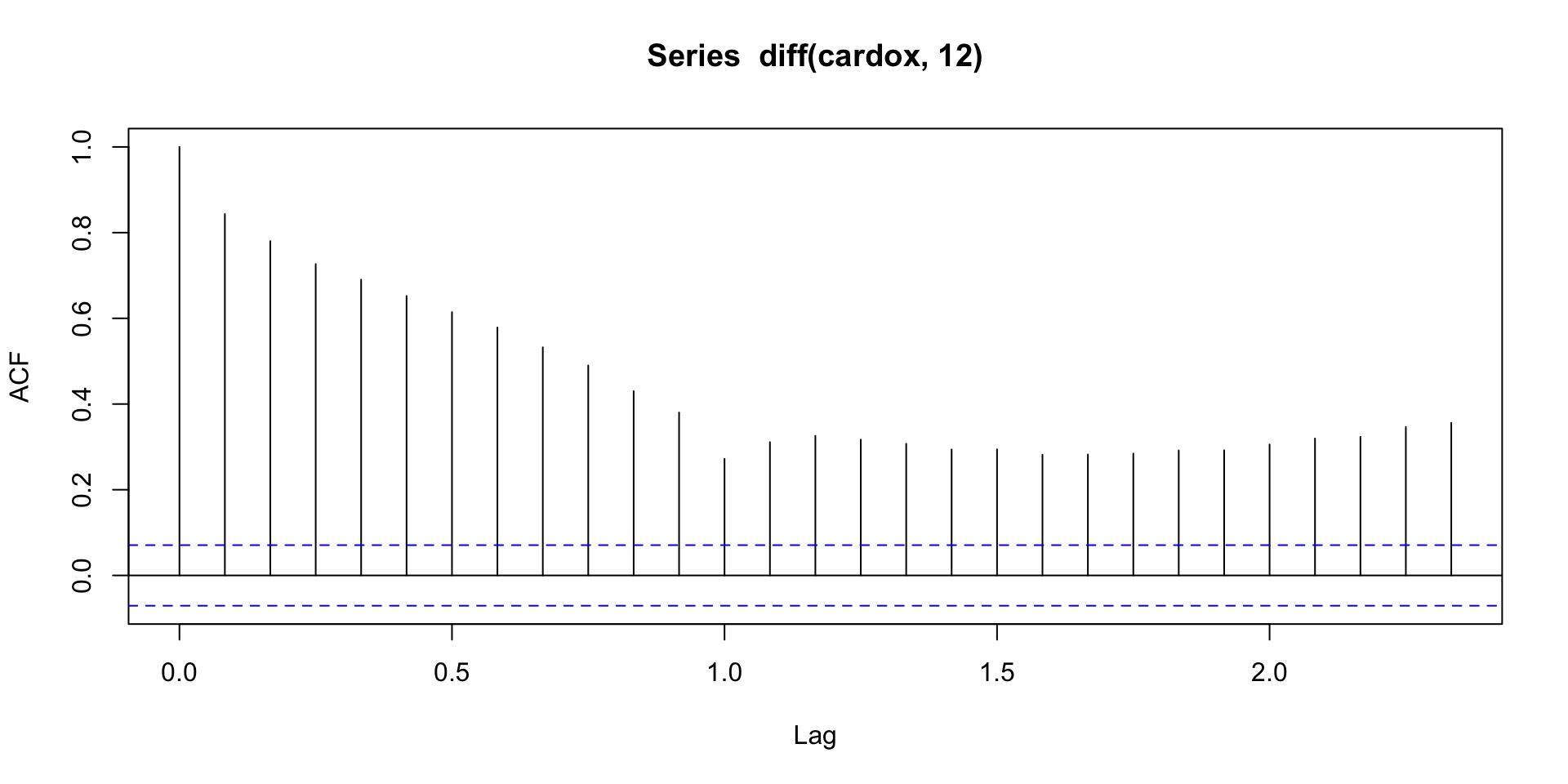
Difference and Seasonal Difference

Looks pretty stationary!

Code

tsplot(diff(diff(cardox, 12)))

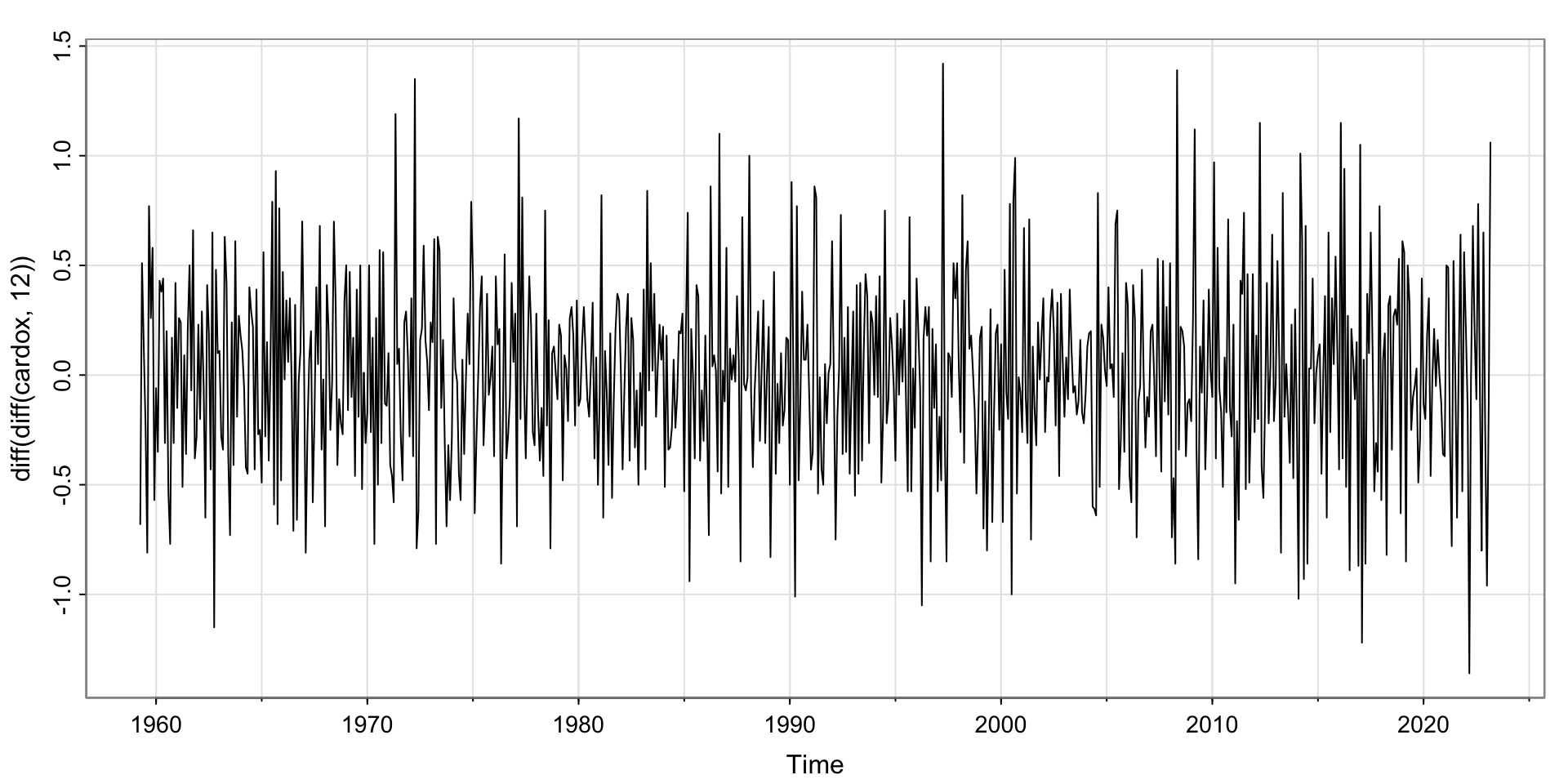
Finding \(p,q\) and \(P,Q\)

We have identified \(d = 1\) and \(D=1\).

SEASONAL: Check acf/pacf for \(P,Q\) and recall the seasonal period (here 12/12 = 1)
NON-SEASONAL: Check acf/pacf for \(p,q\) just like before.

\(p,q\) and \(P,Q\) for Carbon Dioxide

Seasonal: ACF appears to cut off at lag 1 (12 months), but tails of at lags 1, 2, 3, 4– implies a seasonal moving average, so \(Q=1, P= 0\).
Non-seasonal: Appears to cut off at lag 1 (1/12) and PACF tails off. Looks like a MA(1), so \(q = 1, p = 0\).

Code

par(mfrow = c(1,2))
acf1(diff(diff(cardox, 12)))

 [1] -0.30 -0.03 -0.06  0.00  0.00 -0.01  0.03 -0.01  0.05 -0.03  0.19 -0.47
[13]  0.08  0.08  0.00  0.02 -0.05  0.04 -0.04 -0.01 -0.02  0.02 -0.04  0.00
[25]  0.03 -0.06  0.04 -0.03  0.06 -0.03 -0.04  0.04  0.01  0.02  0.00  0.01
[37]  0.04 -0.01 -0.01 -0.01 -0.01 -0.03  0.03  0.03 -0.05  0.00  0.02 -0.02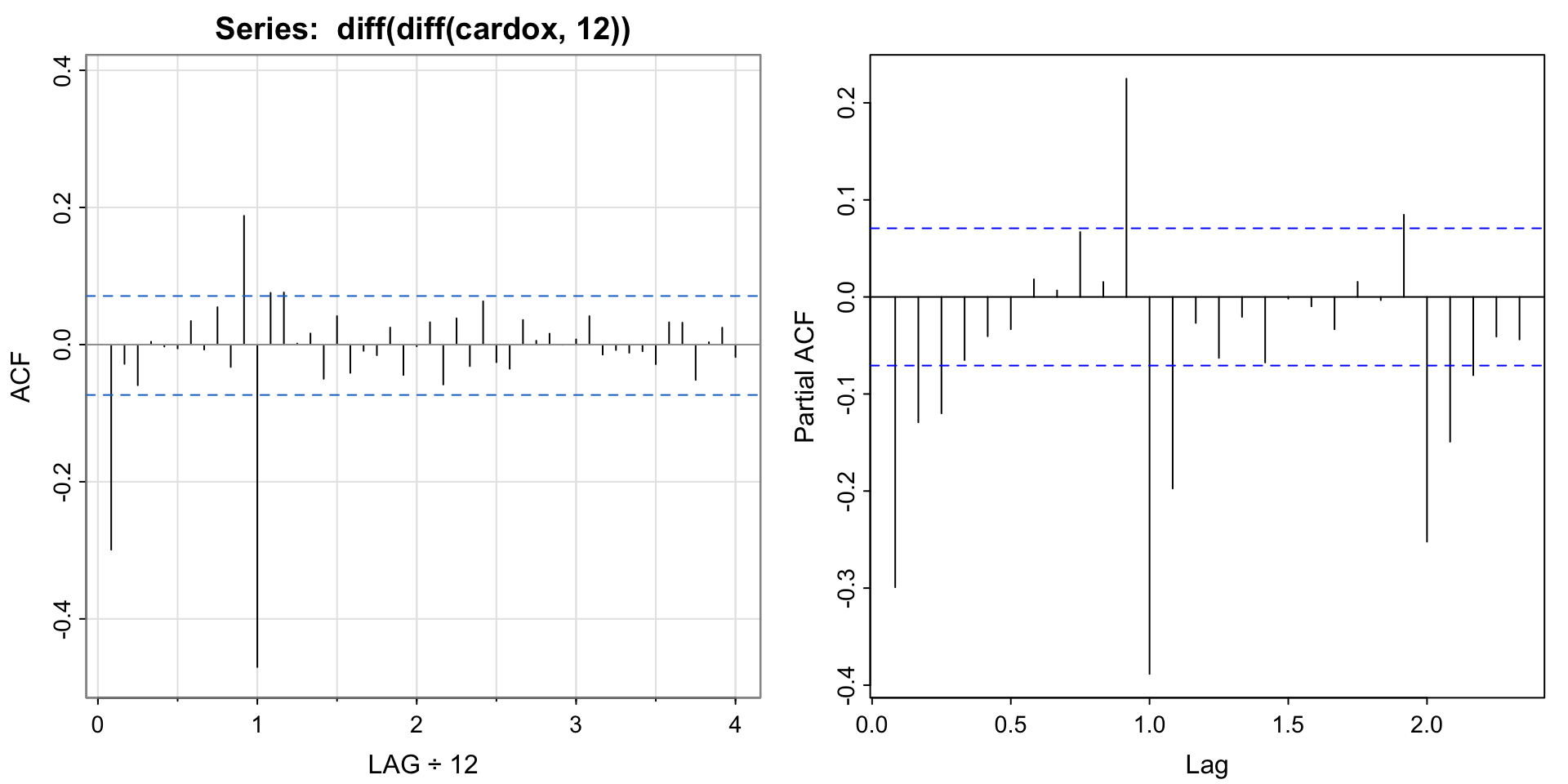

Code

pacf(diff(diff(cardox,12)))

Fit \(ARIMA(0,1,1)\times(0,1,1)_{12}\)

Code

sarima(cardox, p = 0, d = 1, q = 1, P = 0, D = 1, Q = 1, S = 12)

initial  value -0.826338 
iter   2 value -1.059073
iter   3 value -1.093845
iter   4 value -1.116555
iter   5 value -1.124382
iter   6 value -1.126345
iter   7 value -1.127354
iter   8 value -1.127953
iter   9 value -1.127984
iter  10 value -1.127985
iter  10 value -1.127985
iter  10 value -1.127985
final  value -1.127985 
converged
initial  value -1.144615 
iter   2 value -1.148048
iter   3 value -1.148645
iter   4 value -1.149895
iter   5 value -1.150013
iter   6 value -1.150021
iter   7 value -1.150021
iter   7 value -1.150021
iter   7 value -1.150021
final  value -1.150021 
converged
<><><><><><><><><><><><><><>
 
Coefficients: 
     Estimate     SE  t.value p.value
ma1   -0.3869 0.0377 -10.2624       0
sma1  -0.8655 0.0183 -47.2846       0

sigma^2 estimated as 0.0980908 on 766 degrees of freedom 
 
AIC = 0.5456475  AICc = 0.545668  BIC = 0.5637873

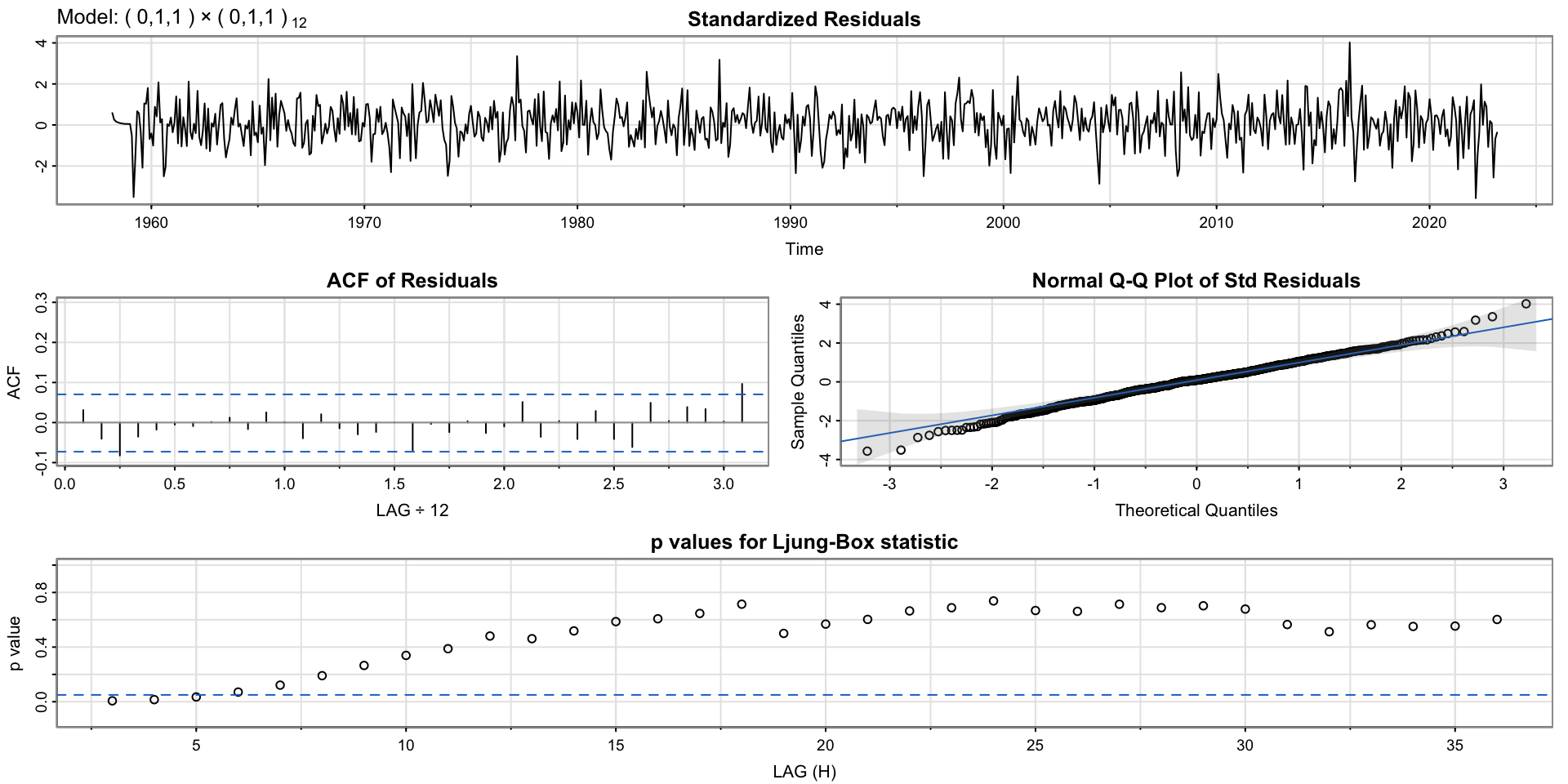
Results

may still have some residual autocorrelation (Ljung-box test for small lags)
Try adding another term? maybe increase order of MA or add AR component?

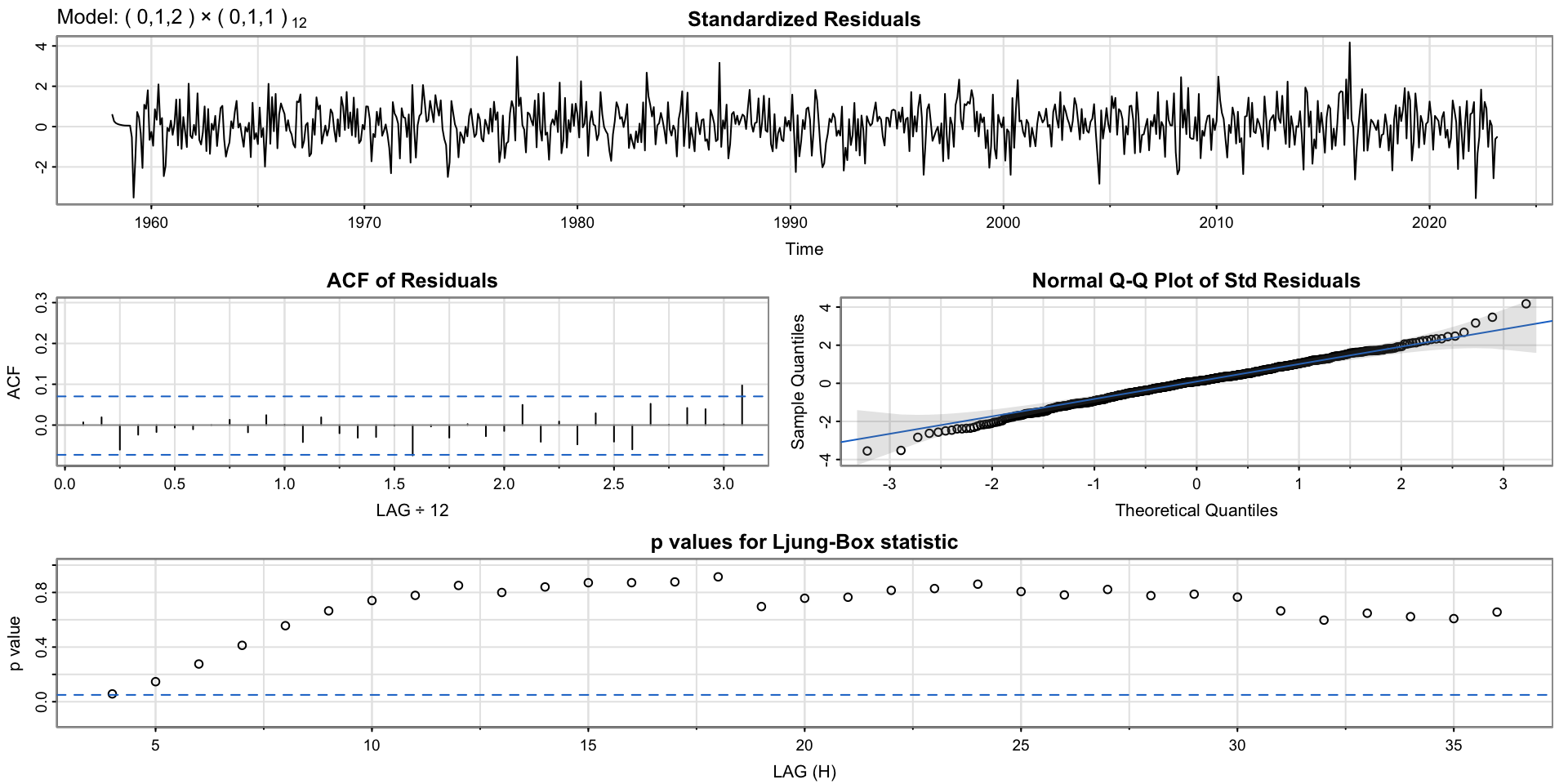
Increase order of MA

Code

sarima(cardox, p = 0, d = 1, q = 2, P = 0, D = 1, Q = 1, S = 12)

initial  value -0.826338 
iter   2 value -1.061232
iter   3 value -1.098226
iter   4 value -1.120391
iter   5 value -1.127720
iter   6 value -1.129516
iter   7 value -1.130690
iter   8 value -1.130938
iter   9 value -1.130955
iter  10 value -1.130959
iter  11 value -1.130959
iter  12 value -1.130959
iter  12 value -1.130959
iter  12 value -1.130959
final  value -1.130959 
converged
initial  value -1.147318 
iter   2 value -1.150711
iter   3 value -1.151405
iter   4 value -1.152442
iter   5 value -1.152564
iter   6 value -1.152573
iter   7 value -1.152574
iter   7 value -1.152574
iter   7 value -1.152574
final  value -1.152574 
converged
<><><><><><><><><><><><><><>
 
Coefficients: 
     Estimate     SE  t.value p.value
ma1   -0.3678 0.0359 -10.2365  0.0000
ma2   -0.0704 0.0354  -1.9911  0.0468
sma1  -0.8651 0.0182 -47.4548  0.0000

sigma^2 estimated as 0.09759346 on 765 degrees of freedom 
 
AIC = 0.5431467  AICc = 0.5431876  BIC = 0.5673331

Code

sarima(cardox, p = 1, d = 1, q = 1, P = 0, D = 1, Q = 1, S = 12)

initial  value -0.827261 
iter   2 value -1.034332
iter   3 value -1.066295
iter   4 value -1.094823
iter   5 value -1.108013
iter   6 value -1.115246
iter   7 value -1.116173
iter   8 value -1.120248
iter   9 value -1.120892
iter  10 value -1.121657
iter  11 value -1.122186
iter  12 value -1.124590
iter  13 value -1.125269
iter  14 value -1.125654
iter  15 value -1.125685
iter  16 value -1.125685
iter  17 value -1.125687
iter  18 value -1.125689
iter  19 value -1.125689
iter  20 value -1.125689
iter  20 value -1.125689
iter  20 value -1.125689
final  value -1.125689 
converged
initial  value -1.146682 
iter   2 value -1.150731
iter   3 value -1.152123
iter   4 value -1.152815
iter   5 value -1.153157
iter   6 value -1.153220
iter   7 value -1.153266
iter   8 value -1.153337
iter   9 value -1.153352
iter  10 value -1.153359
iter  11 value -1.153384
iter  12 value -1.153388
iter  13 value -1.153390
iter  14 value -1.153390
iter  14 value -1.153390
iter  14 value -1.153390
final  value -1.153390 
converged
<><><><><><><><><><><><><><>
 
Coefficients: 
     Estimate     SE  t.value p.value
ar1    0.2203 0.0894   2.4660  0.0139
ma1   -0.5797 0.0753  -7.7029  0.0000
sma1  -0.8656 0.0182 -47.5947  0.0000

sigma^2 estimated as 0.09742764 on 765 degrees of freedom 
 
AIC = 0.541514  AICc = 0.5415549  BIC = 0.5657004

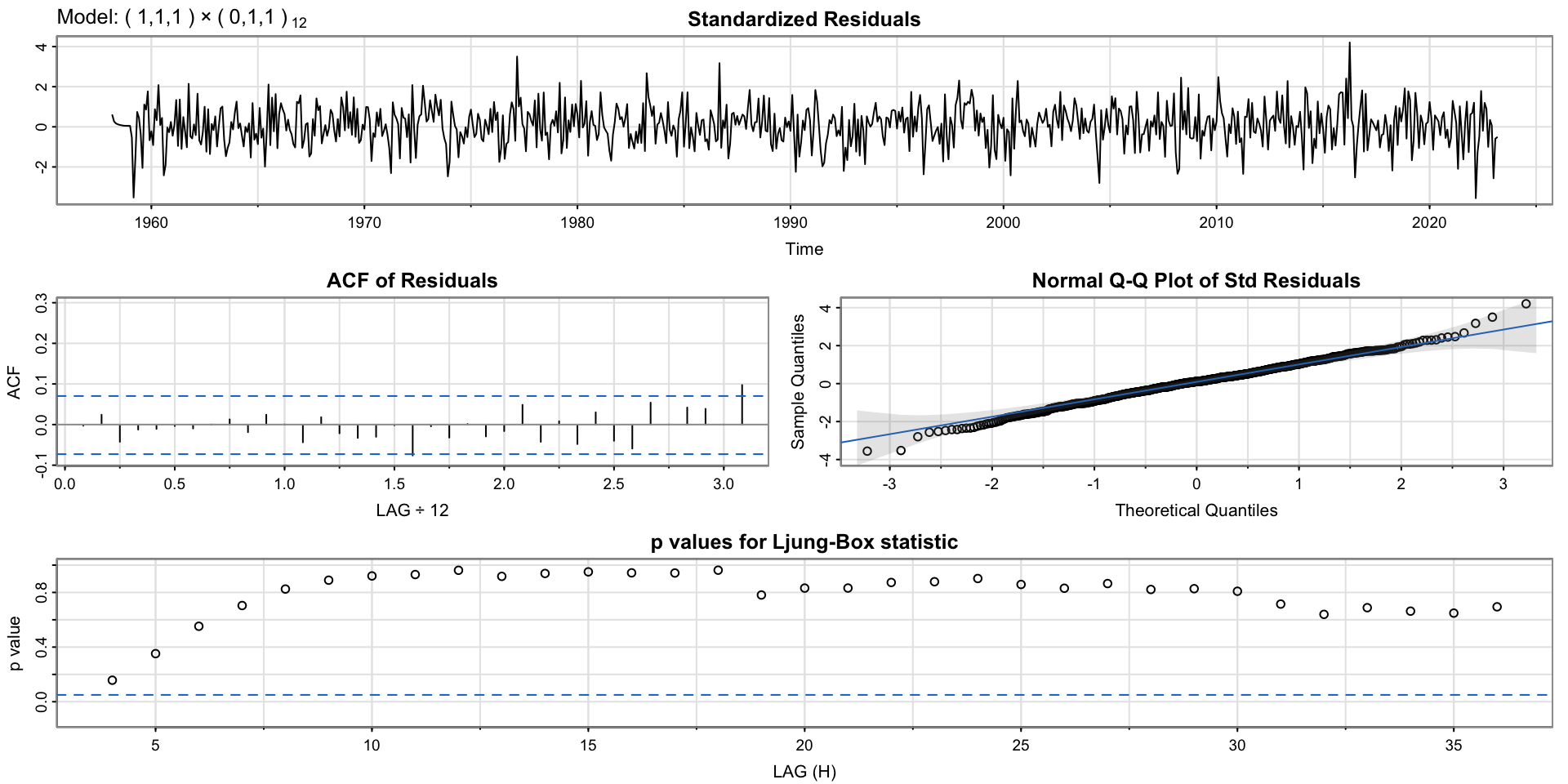
Forecasting

Looks like we predict the \(CO_2\) to continue to increase…

Code

sarima.for(cardox, 60, 1,1,1, 0,1,1,12)

$pred
          Jan      Feb      Mar      Apr      May      Jun      Jul      Aug
2023                            422.5365 423.2516 422.6841 420.8017 418.7844
2024 421.8604 422.7144 423.3343 424.7951 425.4936 424.9223 423.0392 421.0216
2025 424.0976 424.9517 425.5715 427.0323 427.7308 427.1595 425.2764 423.2588
2026 426.3348 427.1889 427.8088 429.2695 429.9680 429.3968 427.5136 425.4961
2027 428.5720 429.4261 430.0460 431.5067 432.2052 431.6340 429.7509 427.7333
2028 430.8092 431.6633 432.2832                                             
          Sep      Oct      Nov      Dec
2023 417.4195 417.6341 419.1994 420.6362
2024 419.6567 419.8713 421.4367 422.8734
2025 421.8940 422.1085 423.6739 425.1106
2026 424.1312 424.3458 425.9111 427.3479
2027 426.3684 426.5830 428.1483 429.5851
2028                                    

$se
           Jan       Feb       Mar       Apr       May       Jun       Jul
2023                               0.3121340 0.3706892 0.4100237 0.4437896
2024 0.6057658 0.6286983 0.6508233 0.6839230 0.7112115 0.7366194 0.7609956
2025 0.8931404 0.9133056 0.9330350 0.9616380 0.9859772 1.0090191 1.0313946
2026 1.1563743 1.1759118 1.1951299 1.2221148 1.2455209 1.2678703 1.2896982
2027 1.4134077 1.4329864 1.4523012 1.4786701 1.5018653 1.5241385 1.5459682
2028 1.6707850 1.6906907 1.7103647                                        
           Aug       Sep       Oct       Nov       Dec
2023 0.4747345 0.5036938 0.5310578 0.5570754 0.5819301
2024 0.7845756 0.8074590 0.8297096 0.8513785 0.8725094
2025 1.0532622 1.0746779 1.0956735 1.1162740 1.1365011
2026 1.3111337 1.3322181 1.3529726 1.3734132 1.3935539
2027 1.5674673 1.5886697 1.6095915 1.6302447 1.6506393
2028

Code

sarima.for(cardox, 60, 1,1,1, 0,1,1,12)

$pred
          Jan      Feb      Mar      Apr      May      Jun      Jul      Aug
2023                            422.5365 423.2516 422.6841 420.8017 418.7844
2024 421.8604 422.7144 423.3343 424.7951 425.4936 424.9223 423.0392 421.0216
2025 424.0976 424.9517 425.5715 427.0323 427.7308 427.1595 425.2764 423.2588
2026 426.3348 427.1889 427.8088 429.2695 429.9680 429.3968 427.5136 425.4961
2027 428.5720 429.4261 430.0460 431.5067 432.2052 431.6340 429.7509 427.7333
2028 430.8092 431.6633 432.2832                                             
          Sep      Oct      Nov      Dec
2023 417.4195 417.6341 419.1994 420.6362
2024 419.6567 419.8713 421.4367 422.8734
2025 421.8940 422.1085 423.6739 425.1106
2026 424.1312 424.3458 425.9111 427.3479
2027 426.3684 426.5830 428.1483 429.5851
2028                                    

$se
           Jan       Feb       Mar       Apr       May       Jun       Jul
2023                               0.3121340 0.3706892 0.4100237 0.4437896
2024 0.6057658 0.6286983 0.6508233 0.6839230 0.7112115 0.7366194 0.7609956
2025 0.8931404 0.9133056 0.9330350 0.9616380 0.9859772 1.0090191 1.0313946
2026 1.1563743 1.1759118 1.1951299 1.2221148 1.2455209 1.2678703 1.2896982
2027 1.4134077 1.4329864 1.4523012 1.4786701 1.5018653 1.5241385 1.5459682
2028 1.6707850 1.6906907 1.7103647                                        
           Aug       Sep       Oct       Nov       Dec
2023 0.4747345 0.5036938 0.5310578 0.5570754 0.5819301
2024 0.7845756 0.8074590 0.8297096 0.8513785 0.8725094
2025 1.0532622 1.0746779 1.0956735 1.1162740 1.1365011
2026 1.3111337 1.3322181 1.3529726 1.3734132 1.3935539
2027 1.5674673 1.5886697 1.6095915 1.6302447 1.6506393
2028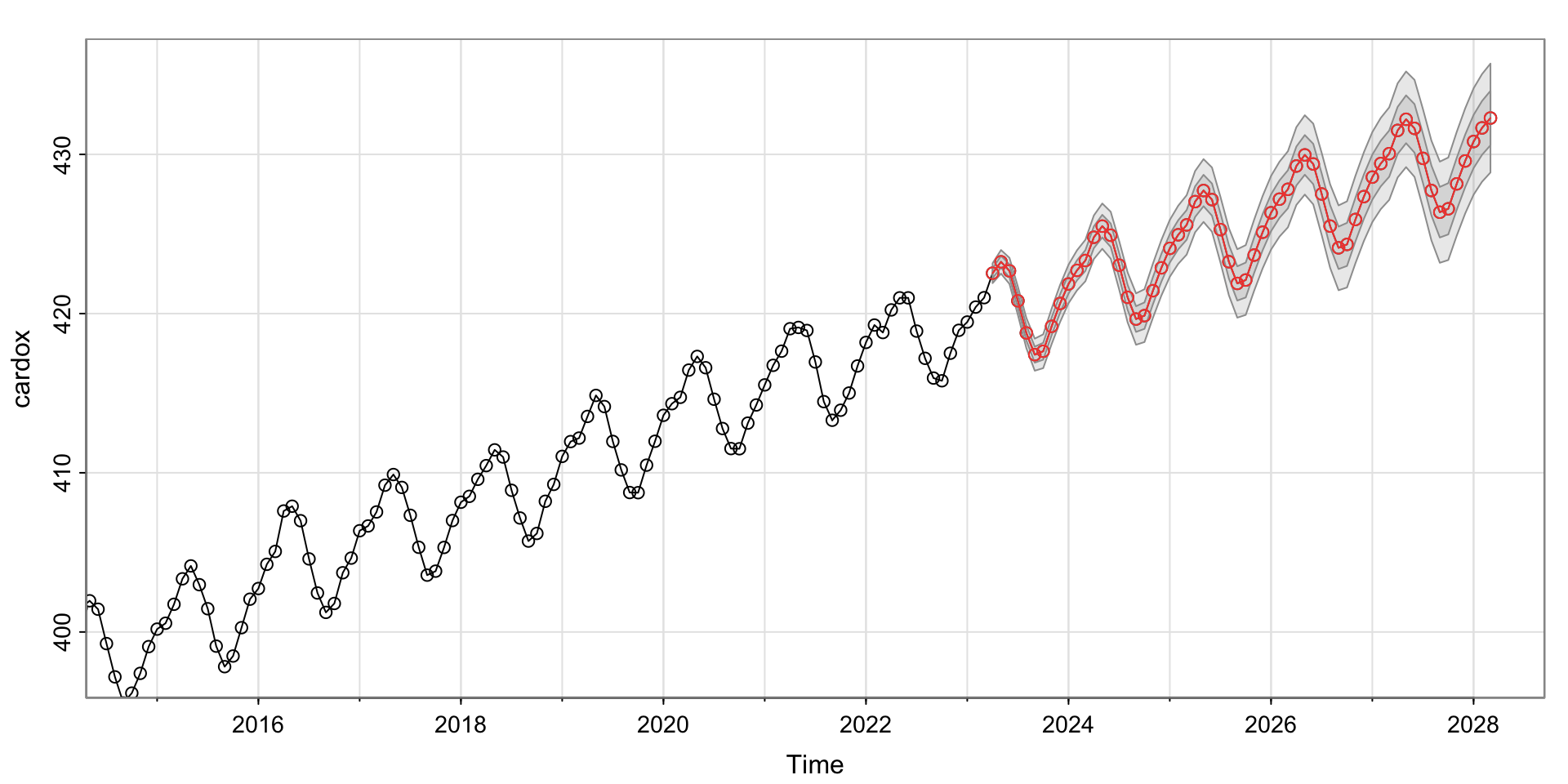

Compare to auto arima

May be overparameterized…

Code

cardox |> 
  as_tsibble() |>
  model(ARIMA(value)) |>
  report()

Series: value 
Model: ARIMA(1,1,1)(2,1,2)[12] 

Coefficients:
         ar1      ma1     sar1     sar2     sma1     sma2
      0.2219  -0.5821  -0.3132  -0.0169  -0.5481  -0.2724
s.e.  0.0891   0.0749   1.4611   0.0421   1.4610   1.2649

sigma^2 estimated as 0.09985:  log likelihood=-203.82
AIC=421.65   AICc=421.79   BIC=454.15

Lecture 11

Announcements

Last time

Is the trend linear?

Try taking the log?

Try differencing?

Unit root tests

What’s a unit?

What’s a root of a polynomial?

What do we care about being one?

Wait, where’s the polynomial? (Advanced topic)

Unit root test in R using features function

Activity 0

In practice

Recall the ARIMA modeling workflow

Activity 1: Manual analysis

Activity 1 Solutions (manual)

Handy table

Activity 1 Solutions (manual)

Activity 1 Solutions

What about automatic?

Specifying \(d\) in the ARIMA call

Going fully automated

Activity 2: Should we go fully automated??

Using the sarima function for diagnostics

Activity 3: p-values for Ljung-Box statistic

Testing if the residuals are white noise

Ljung-box in fable

Seasonal Arima models

Goal: define Seasonal Arima model

Pure Seasonal ARIMA

Simulating a pure seasonal AR(1) process

Hawaiian Quarterly Occupancy

Hawaiian Quarterly Occupancy

Carbon Dioxide Readings

What’s the acf?

Let’s try a seasonal difference!

Check the acf

Difference and Seasonal Difference

Finding \(p,q\) and \(P,Q\)

\(p,q\) and \(P,Q\) for Carbon Dioxide

Fit \(ARIMA(0,1,1)\times(0,1,1)_{12}\)

Results

Increase order of MA

Forecasting

Compare to auto arima

Unit root test in `R` using `features` function

Specifying \(d\) in the `ARIMA` call

Using the `sarima` function for diagnostics

Ljung-box in `fable`