Lecture 2

Julia Schedler

Recap from last time

\[ \newcommand\E{{\mathbb{E}}} \]

• Several examples of time series data sets

• Experience plotting the time series

• Exposure to some common time series models

Today

• Notation review
• Mean and covariance function of a time series
• R code activity
• Stationarity (if time)

Coming up/notices

• I combined the Canvas sections (applies to section 2)
• Quiz 1 posted today, due tomorrow at midnight (20 minutes to do it)
• Assignment 1 will also be posted today, due Monday at midnight (boundary between Monday and Tuesday)
• Next week’s office hours: M 4-5, T 12-2

Review of notation

Notation and Data- White noise

“Let \(w_t\) be a white noise series”

t	Random Variable	Example data
1	\(w_1 \sim N(0, \sigma_w^2)\)	-0.6100677
2	\(w_2 \sim N(0, \sigma_w^2)\)	0.207556
	\(\vdots\)	\(\vdots\)
t	\(w_t \sim N(0, \sigma^2_w)\)	-0.8756262
\(\vdots\)	\(\vdots\)	\(\vdots\)
n	\(w_n \sim N(0, \sigma_w^2)\)	-0.8783702

If we interpret the collection of \(w_t\) as a random vector, then \(w_t \sim MVN(\vec{0}, I)\) (why \(I\)?)

Note: sometimes \(w_t\) could mean a (univariate) value of a white noise series for a particular time \(t\) (kind of like how you refer to an arbitrary \(x_i\) when you have a sample \(x_1, \dots, x_n\)).

(Aside) The Multivariate normal distribution

Let’s look on Wikipedia. What are the parameters?

• mean vector

• variance (covariance) matrix

  • If the covariance matrix is the identity matrix, the the covariances are 0

(Aside) Bivariate normal distribution for uncorrelated case

# install.packages("ggplot2")
# install.packages("ggExtra")
library(ggplot2)
library(ggExtra)

x1 <- rnorm(100, 10, 5)
x2 <- rnorm(100, .1, .5)

x <- data.frame(x1, x2)
# Save the scatter plot in a variable
p <- ggplot(x, aes(x = x1, y = x2)) +
  geom_point()

# Arguments for each marginal histogram
ggMarginal(p, type = "histogram", 
           xparams = list(fill = 4),
           yparams = list(fill = 3))

(Aside) Bivariate normal distribution for correlated case

#install.packages("MASS")
library(MASS)

mu <- c(10, .1)
varcov <- matrix(c(5, 1, 1, .5), 
                 ncol = 2)
x<- mvrnorm(100, mu = mu, Sigma =varcov)
x <- data.frame(x1 = x[,1], x2 = x[,2])
# Save the scatter plot in a variable
p <- ggplot(x, aes(x = x1, y = x2)) +
  geom_point()

# Arguments for each marginal histogram
ggMarginal(p, type = "histogram", 
           xparams = list(fill = 4),
           yparams = list(fill = 3))

Building time series models from White Noise

Model	Inputs	Output
White noise	probability distribution, independence assumption, \(\sigma_w^2\)
Moving average with \(p\) points	\(w_1, w_2, \dots, w_n\)
Autoregression of order \(p\)	\(w_1, w_2, \dots, w_n\) and \(\phi = (\phi_1, \dots, \phi_p)\)
Random walk with drift	\(w_1, w_2, \dots, w_n\) and \(\delta\)
Signal plus noise	\(w_1, w_2, \dots, w_n\) and a function \(f(t)\)

Identify which of the inputs are random variables, pre-specified constants, pre-specified functions, or parameters to be estimated.

Building time series models from White Noise

Model	Inputs	Output
White noise	probability distribution, independence assumption, \(\sigma_w^2\)	\(w_1, w_2, \dots, w_n\); for each \(t = 1, \dots, n\) we have \(w_t \sim N(0, \sigma^2_w)\)
Moving average with \(p\) points	\(w_1, w_2, \dots, w_n\)	\(v_t = \frac{1}{p}\sum_{i = 1}^{p} w_{t-(p-i)}\)
Autoregression of order \(p\)	\(w_1, w_2, \dots, w_n\) and \(\phi = (\phi_1, \dots, \phi_p)\)	\(x_t = \sum_{i = 1}^p \phi_ix_{t-i} + w_t\)
Random walk with drift	\(w_1, w_2, \dots, w_n\) and \(\delta\)	\(x_t = \delta + x_{t-1} + w_t\)
Signal plus noise	\(w_1, w_2, \dots, w_n\) and a function \(f(t)\)	\(x_t = f(t) + w_t\)

Identify which of the inputs are random variables, pre-specified constants, pre-specified functions, or parameters to be estimated.

Notation and Data

Consider the general version of the autoregressive model of order 1:

\[ x_t = \phi_1x_{t-1} + \phi_2x_{t-2} + w_t \]

If you had data representing this process, what would it look like in R?

Notation and Data

Suppose \(\phi_1 = 1.5\) and \(\phi_2 = -0.75\).

set.seed(90210)
w = rnorm(250 + 50) # 50 extra to avoid startup problems
x = filter(w, filter=c(1.5,-.75), method="recursive")[-(1:50)]
x

  [1] -0.635871231 -3.159366457 -3.336983558 -0.670017029  1.928041062
  [6]  6.262719337  8.811276769  6.994297589  6.964249838  4.172630149
 [11]  0.109387891 -2.838470465 -3.650839732 -5.293859716 -4.924149166
 [16] -3.496962661 -0.001206165  3.982335012  5.166059171  5.391303364
 [21]  4.598152813  2.726933281 -0.656314289 -2.634587218 -3.070392399
 [26] -2.447369835 -2.377035961 -3.272222376 -2.212579163 -1.609152064
 [31]  0.088151906  1.834292884  1.566977751  1.162326919  1.731270484
 [36]  0.452095019  0.751851590  2.197474589  2.037090911  2.053962776
 [41]  1.057859241  0.173798276 -1.559467228 -1.275347235 -1.934447794
 [46] -0.637721288  1.108281203  1.703590245  2.757116948  3.535041828
 [51]  2.785518718 -0.255025902 -3.601017151 -5.665073618 -5.320832378
 [56] -3.801870752 -1.843797185  0.540063136  1.577259338  2.719389114
 [61]  2.386440948  0.360417214  0.130240105  1.213682241  0.970840444
 [66]  1.672645132  1.169230978 -0.197824215 -0.552895930  0.483295378
 [71]  2.002207259  2.483139041  4.761206339  7.166338800  7.329547964
 [76]  5.238955522  1.955859515 -1.445155254 -3.624225029 -3.976740747
 [81] -2.522488940 -0.560280191  1.716462129  2.956985039  3.167747954
 [86]  2.655920142  2.503263867  0.243980727 -1.733850533  0.218414375
 [91]  1.212655465  1.188737220 -0.024525903  0.824315000 -0.929797989
 [96] -3.643408960 -4.872924684 -5.365789994 -4.379073769 -0.816292614
[101]  2.069716217  3.317790830  4.024356559  4.445225438  4.807260941
[106]  3.077726417  0.597309443 -1.889650709 -3.193428803 -4.189085934
[111] -5.056410971 -5.113692514 -1.701862879  0.197898712  1.872046685
[116]  2.519653174  1.995693810  1.375972346  2.342728546  1.412737664
[121] -1.604693814 -4.224595521 -6.808370201 -8.238970434 -7.267053979
[126] -5.073807901 -0.614874790  1.926334410  3.620792660  4.301297376
[131]  2.938794190  2.482699730  2.062144627  0.145550378 -2.263580334
[136] -3.515516041 -5.626740964 -5.675586843 -5.285219511 -3.877662550
[141] -2.843191932 -2.159754220 -1.134175851  0.621526810  2.144676177
[146]  1.301986893  1.090681772  0.483465932 -1.699760373 -0.907358670
[151] -1.964189610 -2.083464483 -2.401372850 -1.102177741  0.090984198
[156]  1.539763874  1.675986590  1.340872200 -0.451023892 -1.070116007
[161] -1.485934032  0.223487236  2.011408533  1.630095949  3.323091734
[166]  4.997983168  5.156394449  4.241727271  0.336603262 -1.668930450
[171] -3.056412007 -2.346607210  0.799083342  0.765047225  0.480923824
[176]  0.301524245  1.422952841  2.820001236  3.981388964  2.988835261
[181] -0.058956147 -2.066827932 -4.518505369 -5.447774381 -5.746818410
[186] -5.473607376 -3.515892394  0.432262861  4.283988479  6.685899229
[191]  6.379550991  5.781828167  5.127569880  2.228597185  1.512254758
[196]  1.407053783 -0.275040161 -2.623401872 -4.707758722 -6.845203817
[201] -8.189848947 -8.441072069 -5.100352049 -1.929194703 -0.289395357
[206]  2.511067946  4.007902754  2.638931037  0.953911823 -0.914044608
[211] -3.131803887 -4.574239309 -4.239263041 -1.278975512 -1.720543477
[216] -1.393708189 -0.978071153 -0.052109821 -0.479546542 -1.072444773
[221] -1.940146902 -2.221618511 -1.892476988 -0.145214604  1.941929437
[226]  2.662695670  1.548128421  1.266366609 -1.415637008 -2.255649300
[231] -2.492380384 -1.758574495 -0.272146596  1.472164787  1.788881267
[236]  0.946614002 -0.426152284  0.059796487 -2.263388225 -4.255693202
[241] -5.023127496 -5.240398677 -5.705131625 -3.494170488 -0.385992861
[246]  1.270003055  3.142585019  5.720389808  5.393790259  1.711581565

R example - Moving Average

set.seed(70)

# generate white noise
w_t <- rnorm(10, 0, 1)

## manually lag terms
w_t1 <- c(NA, w_t[1:9])
w_t2 <- c(NA, NA, w_t[1:8])

## manually compute MA(3)
v_t <- (w_t + w_t1 + w_t2)/3

## compare the vectors
ma_3 <- cbind(v_t, w_t, w_t1, w_t2)
round(ma_3, 3)

         v_t    w_t   w_t1   w_t2
 [1,]     NA -1.542     NA     NA
 [2,]     NA  0.347 -1.542     NA
 [3,] -0.032  1.099  0.347 -1.542
 [4,]  0.316 -0.499  1.099  0.347
 [5,] -0.112 -0.938 -0.499  1.099
 [6,] -0.523 -0.132 -0.938 -0.499
 [7,] -0.265  0.276 -0.132 -0.938
 [8,] -0.087 -0.405  0.276 -0.132
 [9,] -0.609 -1.696 -0.405  0.276
[10,] -0.569  0.394 -1.696 -0.405

R example - Moving Average

# generate white noise
n = 50
w_t <- rnorm(n, 0, 1)

## manually lag terms
w_t1 <- c(NA, w_t[1:(n-1)])
w_t2 <- c(NA, NA, w_t[1:(n-2)])

## manually compute MA(3)
v_t <- (w_t + w_t1 + w_t2)/3

## compare the vectors
ma_3 <- cbind(v_t, w_t, w_t1, w_t2)
round(ma_3, 3)

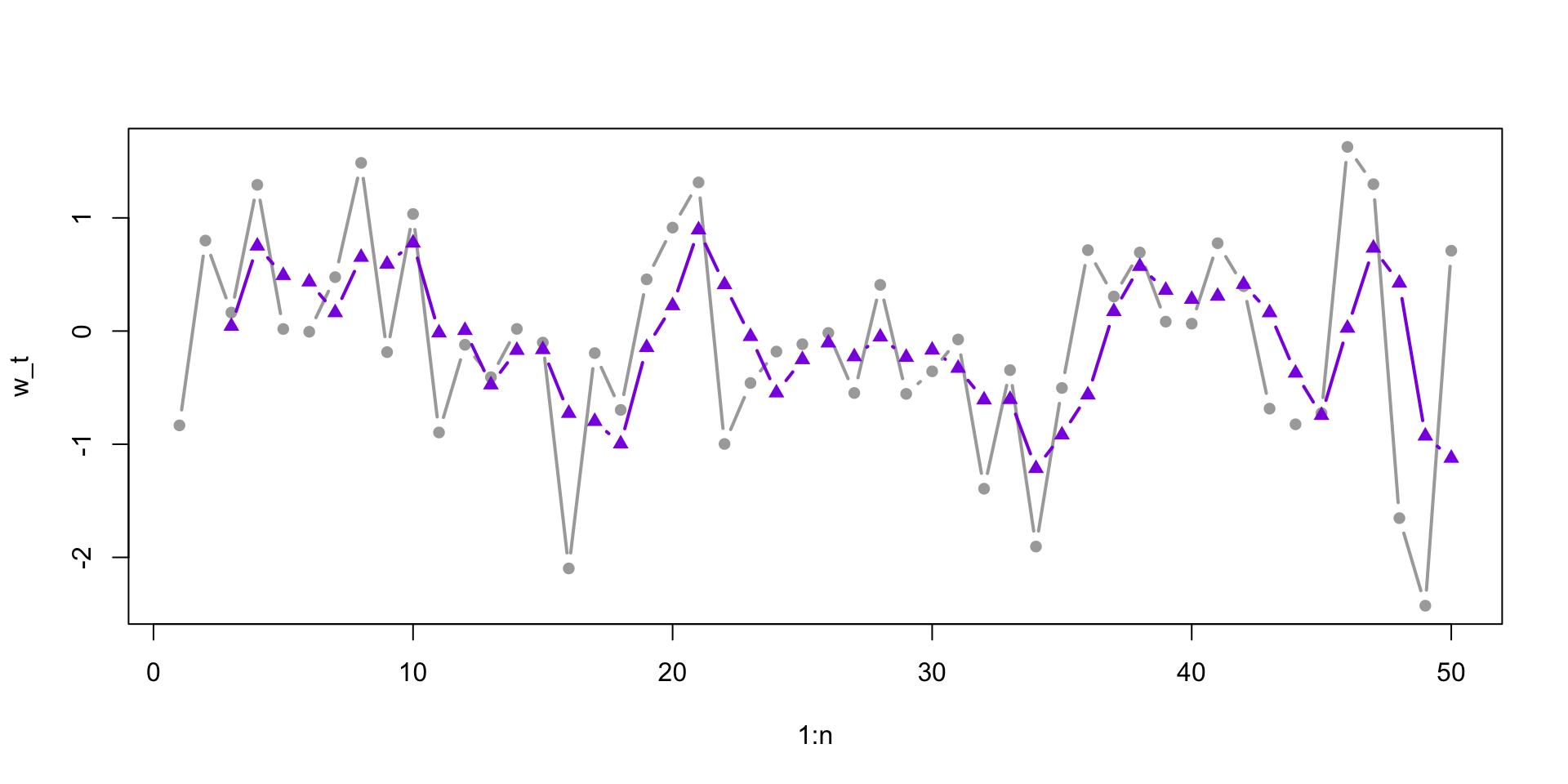
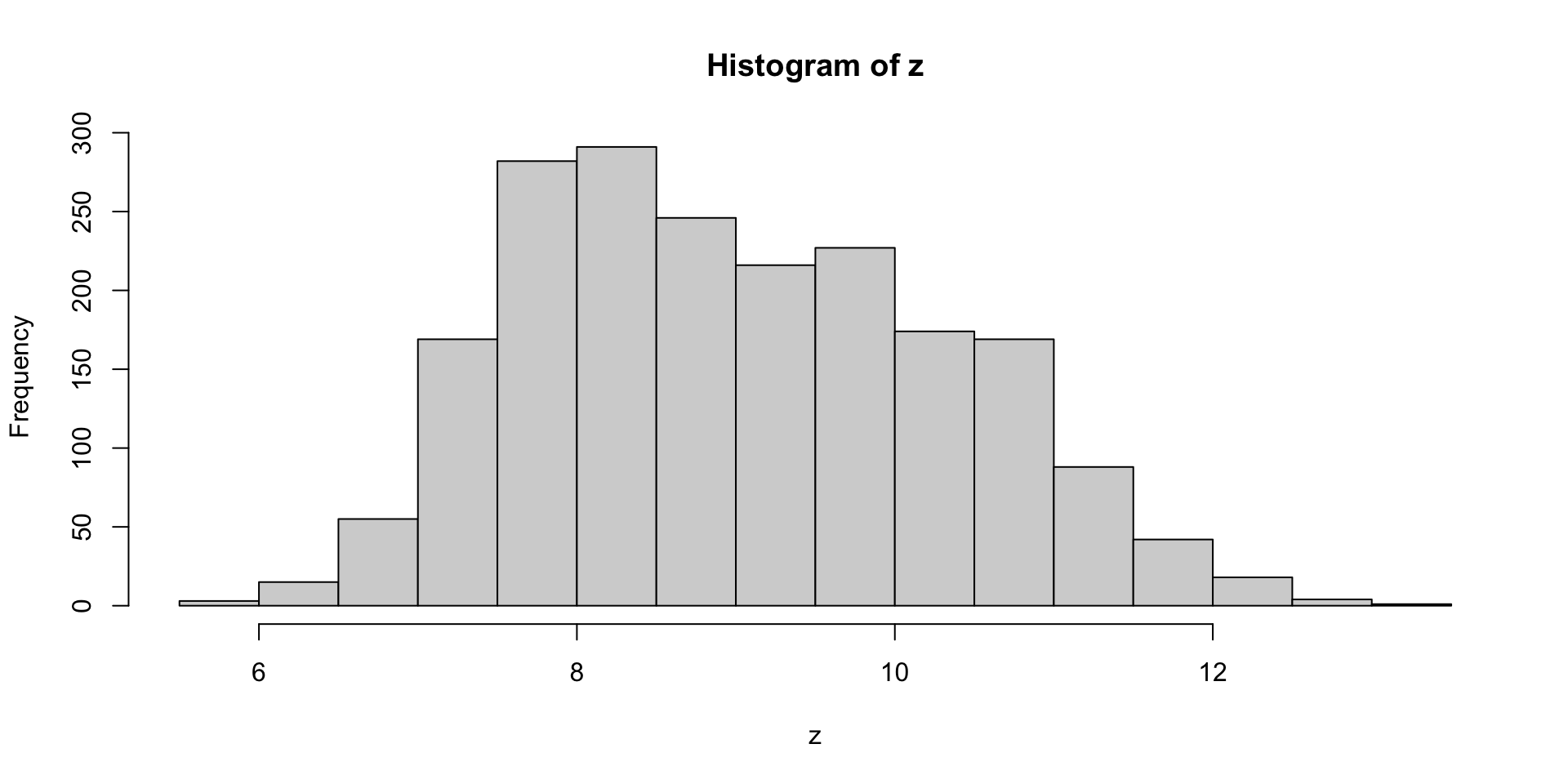
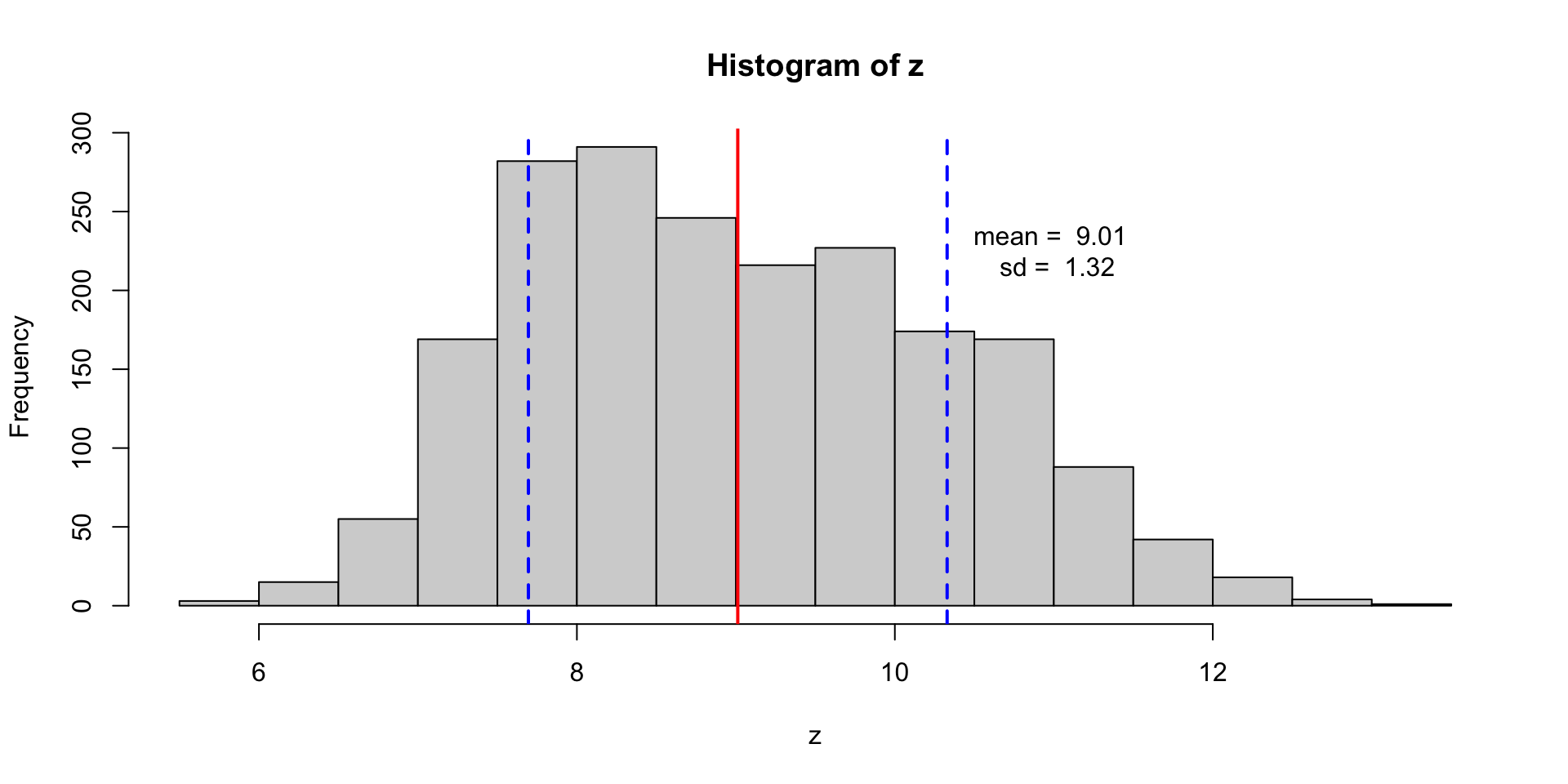
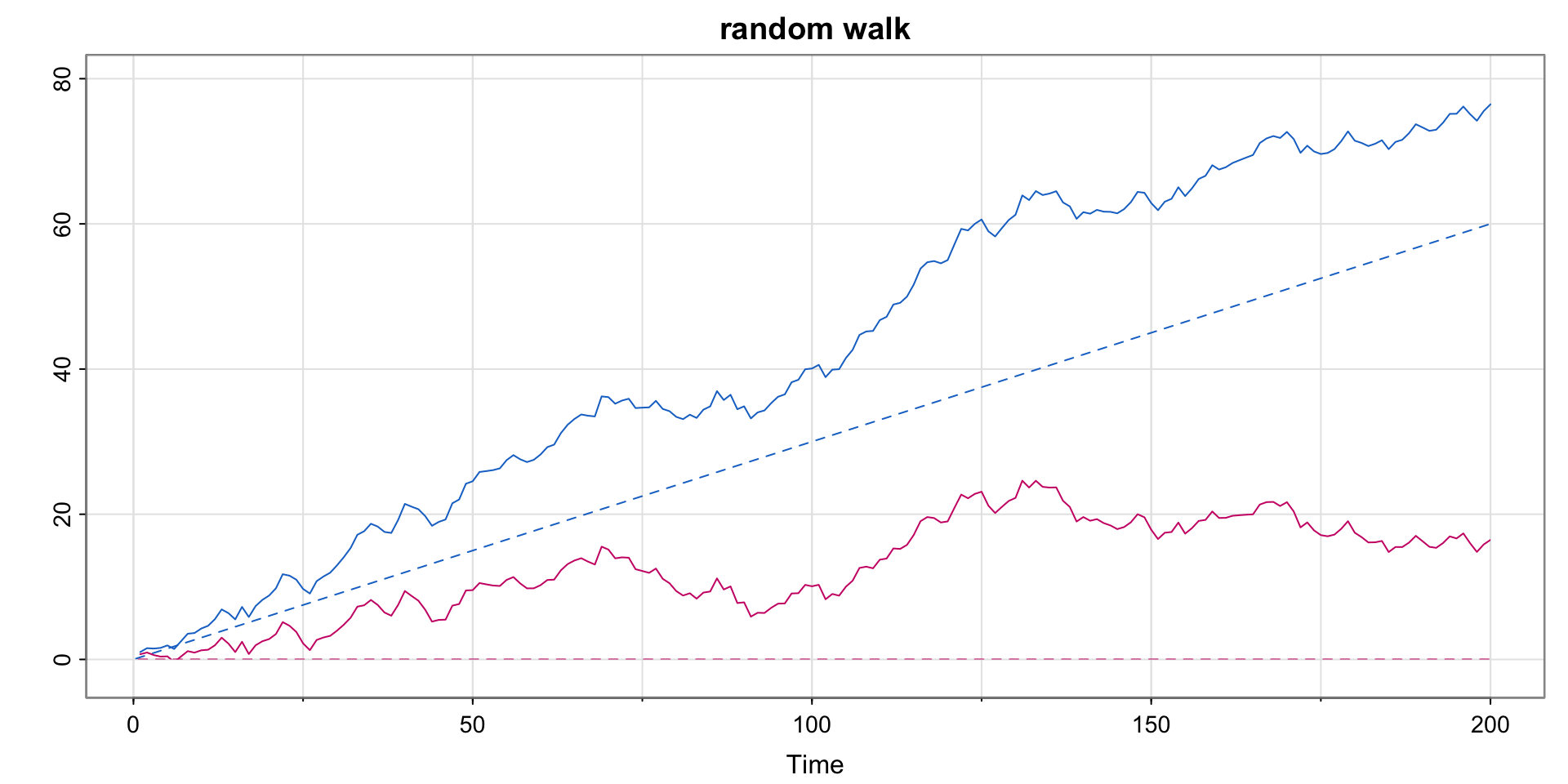
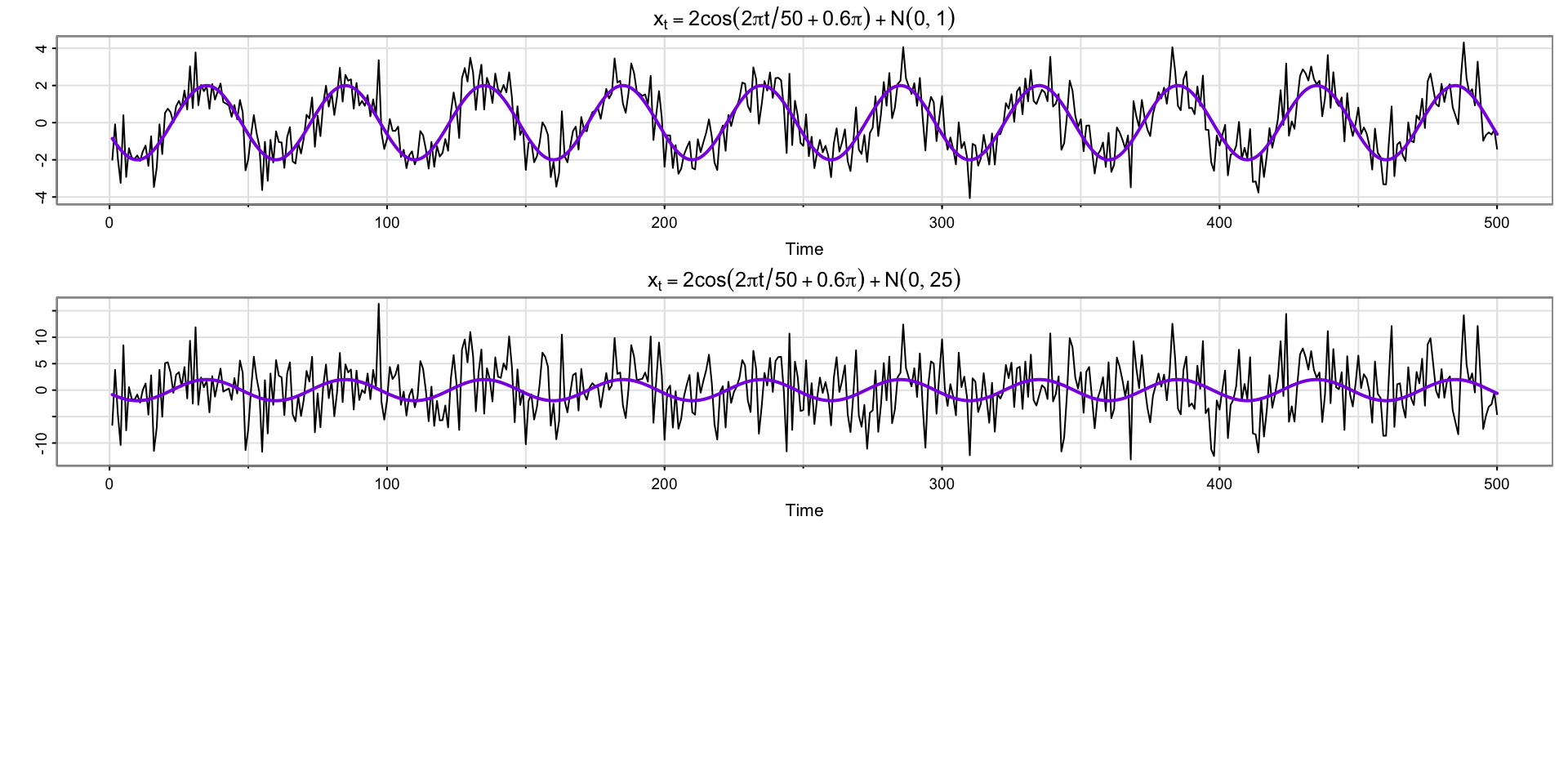
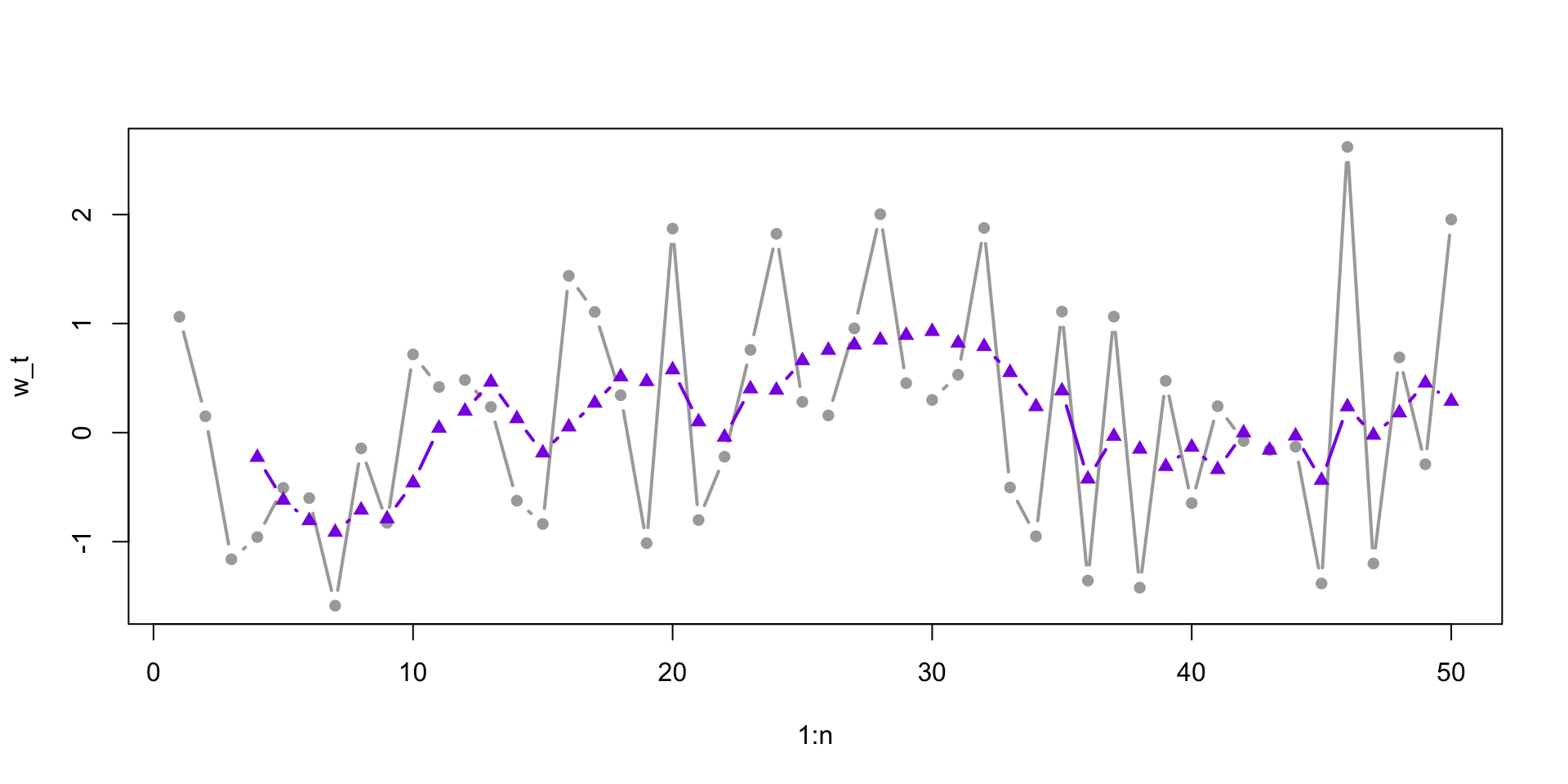
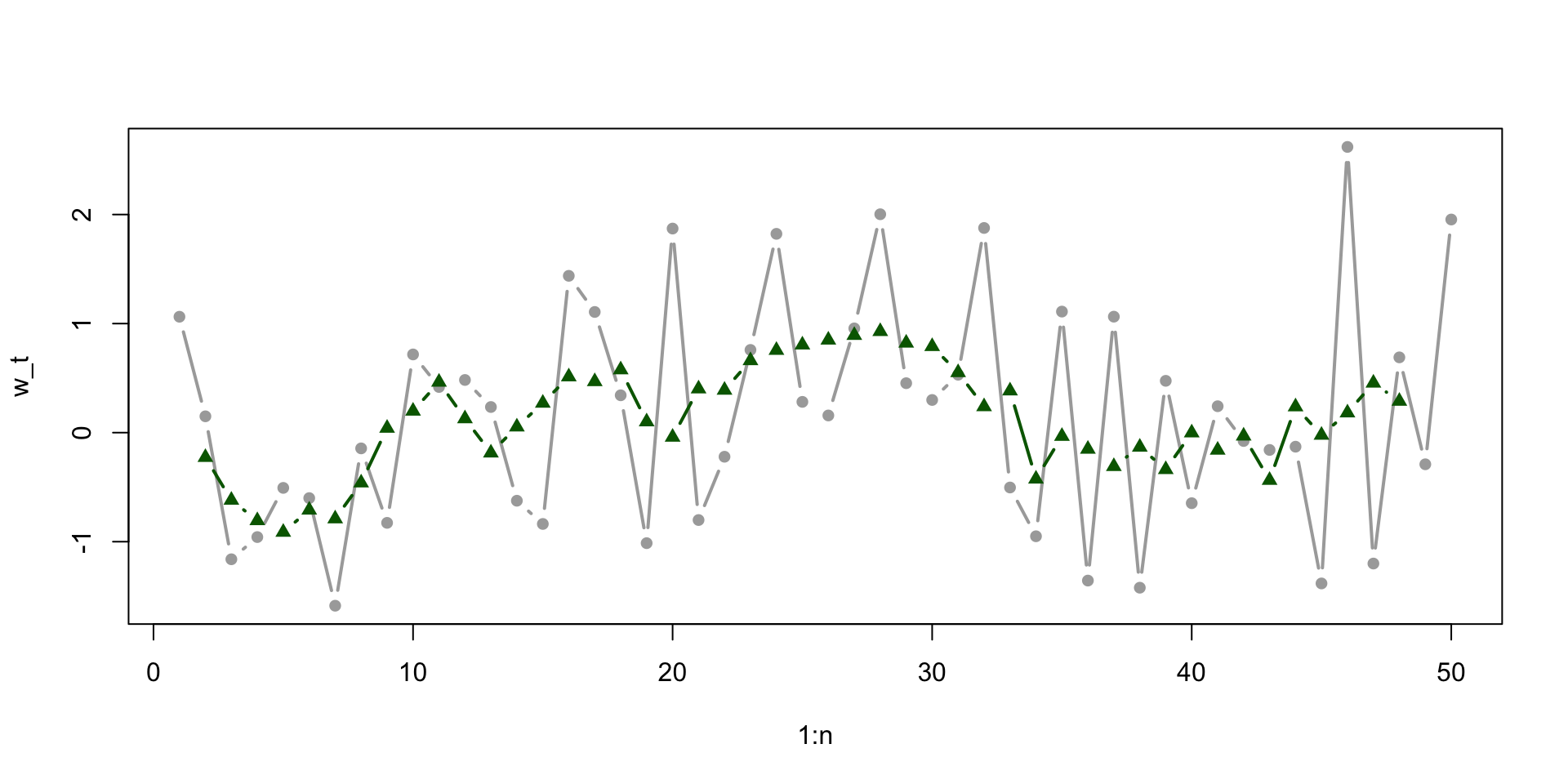
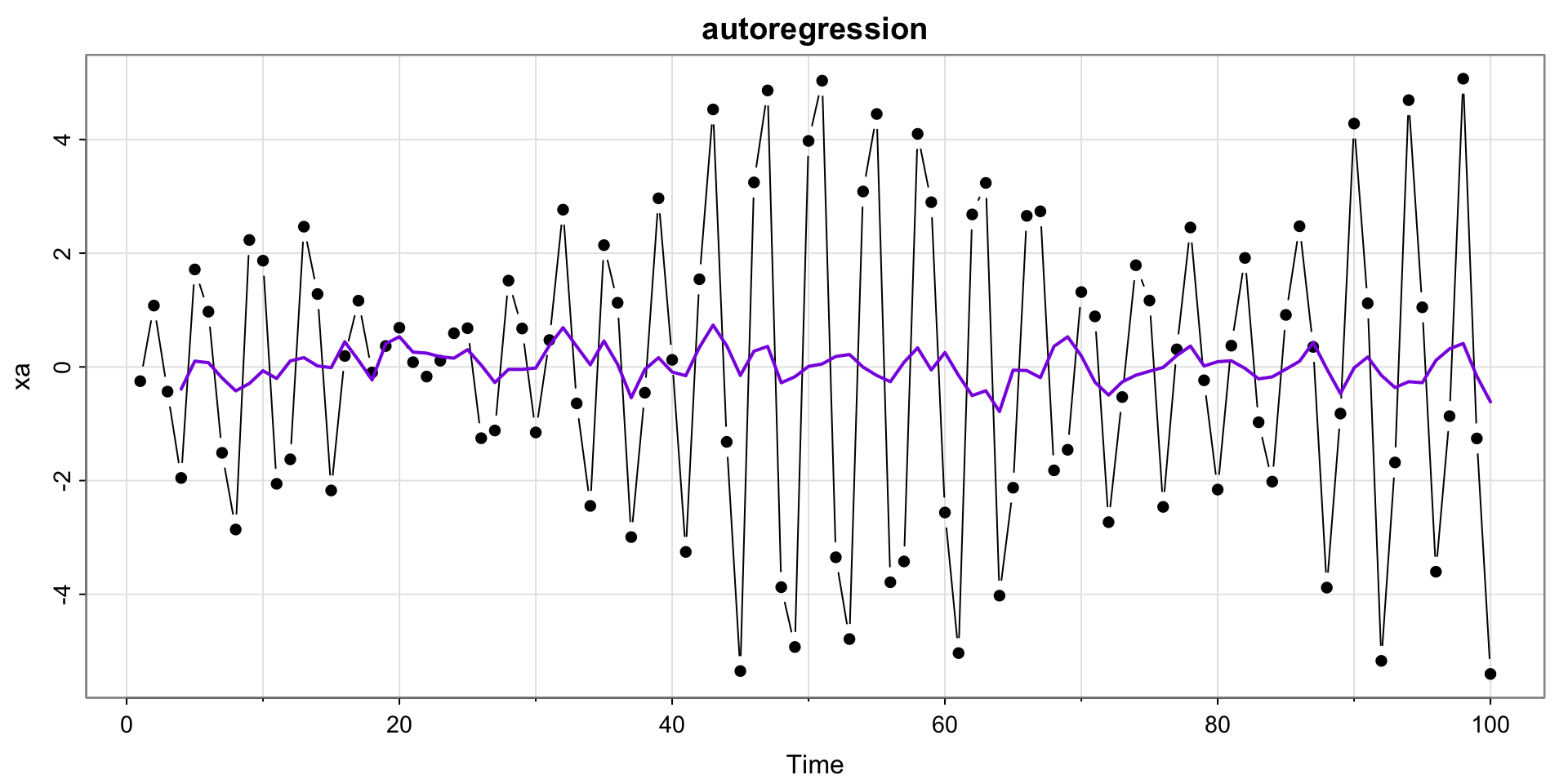
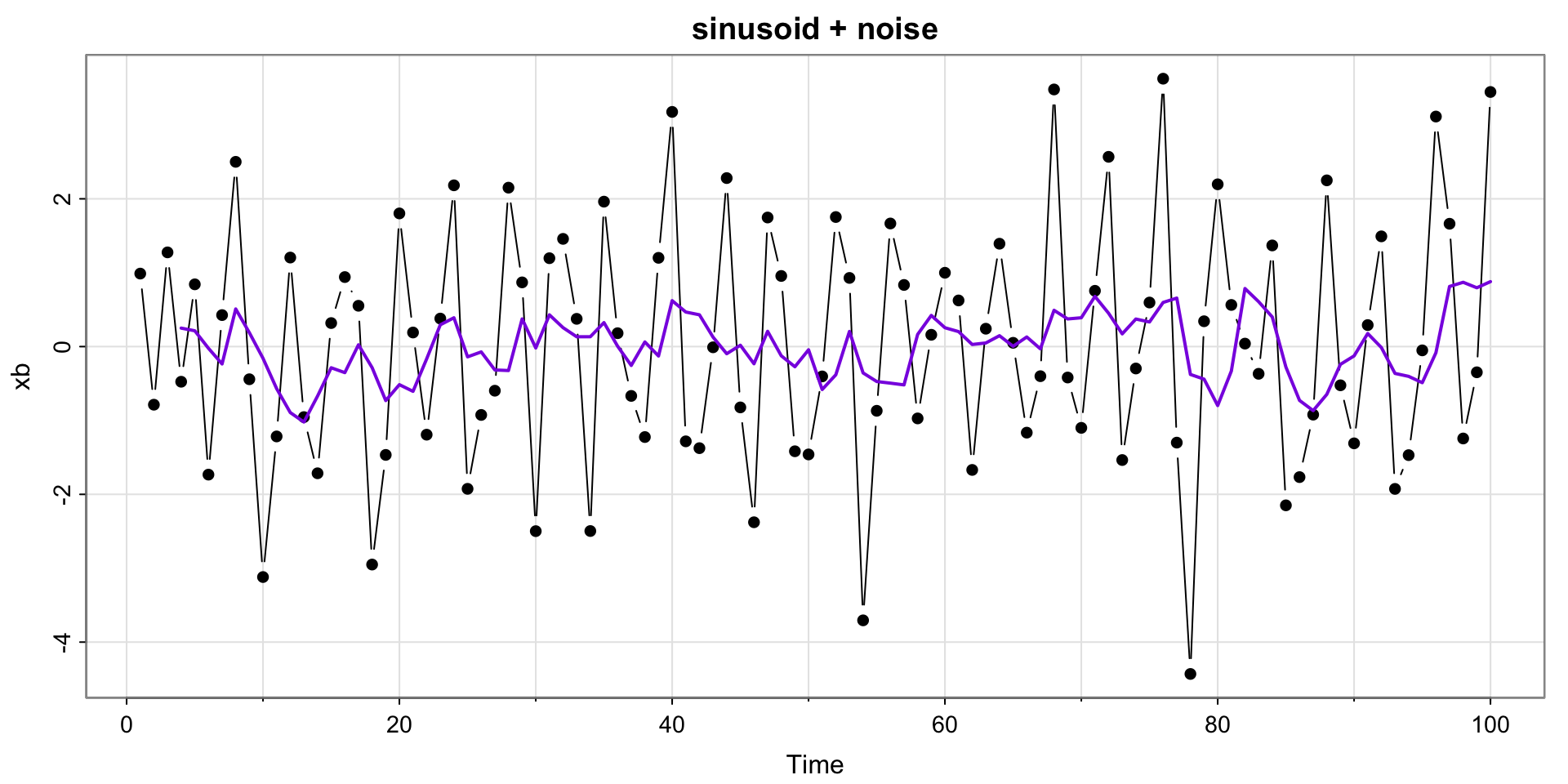
         v_t    w_t   w_t1   w_t2
 [1,]     NA -0.834     NA     NA
 [2,]     NA  0.799 -0.834     NA
 [3,]  0.043  0.163  0.799 -0.834
 [4,]  0.752  1.292  0.163  0.799
 [5,]  0.491  0.018  1.292  0.163
 [6,]  0.435 -0.006  0.018  1.292
 [7,]  0.163  0.476 -0.006  0.018
 [8,]  0.652  1.486  0.476 -0.006
 [9,]  0.592 -0.186  1.486  0.476
[10,]  0.778  1.034 -0.186  1.486
[11,] -0.016 -0.896  1.034 -0.186
[12,]  0.006 -0.121 -0.896  1.034
[13,] -0.475 -0.408 -0.121 -0.896
[14,] -0.170  0.019 -0.408 -0.121
[15,] -0.164 -0.102  0.019 -0.408
[16,] -0.727 -2.098 -0.102  0.019
[17,] -0.798 -0.195 -2.098 -0.102
[18,] -0.996 -0.697 -0.195 -2.098
[19,] -0.145  0.457 -0.697 -0.195
[20,]  0.225  0.914  0.457 -0.697
[21,]  0.895  1.314  0.914  0.457
[22,]  0.410 -0.998  1.314  0.914
[23,] -0.048 -0.459 -0.998  1.314
[24,] -0.546 -0.181 -0.459 -0.998
[25,] -0.252 -0.116 -0.181 -0.459
[26,] -0.105 -0.017 -0.116 -0.181
[27,] -0.227 -0.547 -0.017 -0.116
[28,] -0.052  0.408 -0.547 -0.017
[29,] -0.231 -0.555  0.408 -0.547
[30,] -0.168 -0.356 -0.555  0.408
[31,] -0.328 -0.074 -0.356 -0.555
[32,] -0.608 -1.393 -0.074 -0.356
[33,] -0.604 -0.345 -1.393 -0.074
[34,] -1.214 -1.904 -0.345 -1.393
[35,] -0.917 -0.503 -1.904 -0.345
[36,] -0.564  0.715 -0.503 -1.904
[37,]  0.173  0.306  0.715 -0.503
[38,]  0.572  0.694  0.306  0.715
[39,]  0.361  0.083  0.694  0.306
[40,]  0.281  0.065  0.083  0.694
[41,]  0.308  0.776  0.065  0.083
[42,]  0.413  0.397  0.776  0.065
[43,]  0.162 -0.686  0.397  0.776
[44,] -0.371 -0.824 -0.686  0.397
[45,] -0.745 -0.725 -0.824 -0.686
[46,]  0.026  1.627 -0.725 -0.824
[47,]  0.733  1.298  1.627 -0.725
[48,]  0.424 -1.653  1.298  1.627
[49,] -0.927 -2.427 -1.653  1.298
[50,] -1.123  0.710 -2.427 -1.653

Chapter 2: Correlation and Stationary Time Series

Motivation

How do we summarize characteristics of a distribution?

Motivation

How do we summarize characteristics of a distribution?

• mean

• variance(standard deviation)

How do we summarize the characteristics of a distribution that changes over time?

• mean function (of time)

• (auto)(co)variance function (of time)

Mean function

Mean Function

The mean function of a time series \(x_t\) is defined as:

\[ \mu_{xt} = \E(x_t) = \int_{-\infty}^\infty x_tf(x_t)dx_t, \]

where \(\E\) is the expected value operator, shown here for the case of a continuous \(x_t\).

So, for example, if \(x_t\) is normally distributed then \(f\) here would be the normal probability density function (p.d.f.).

Visual examples

Visual examples

Notating the mean function

“When no confusion exists about which time series we are referring to, we will drop a subscript and write \(\mu_{xt}\) as \(\mu_t\).”

Confusion might exist if we have two time series e.g. if

• \(x_t\) is the SOI for a given month and

• \(y_t\) is the estimated new fish for a given month

we would have two mean functions, \(\mu_{yt}\) and \(\mu_{xt}\).

Example 2.2 Mean Function of a Moving Average Series

Let \(w_t\) denote a white noise series.

• What is \(\mu_{wt} = \E(w_t)\) ?

Let \(v_t = \frac{1}{3}(w_{t-1} + w_{t} + w_{t+1})\) .

• What is \(\mu_{vt} = \E(v_t)\)?

(why not just write \(\mu_t\) on this slide?)

Example 2.3 Mean Function of a Random Walk with drift

Look, it’s our friend the random walk with drift (maybe):

\[ x_t = \delta t + \sum_{j = 1}^t w_j \]

What is the mean function of \(x_t\)?

Break

• I saw several turkeys this morning
• I saw someone almost die on a skateboard

Autocovariance

Does the mean function tell us anything about the (in)dependence of the time series?

No (expected value is such a friendly operator!)

Review: Variance and Covariance

If \(X\) is a random variable and then \(\E(X) = \mu\),

\[ Var(X) = \E((X-\mu)^2) \] If we have two random variables \(X_\alpha\) and \(X_\beta\), the covariance between these is \[ Cov(X_\alpha, X_\beta) = \E[(X_\alpha - \mu_\alpha)(X_\beta - \mu_\beta)] \] - remember correlation (scaled covariance)??

Autocovariance function

The autocovariance function is defined as the second moment product \[ \gamma_x(s, t) = cov(x_s, x_t) = \E[(x_s - \mu_s)(x_t - \mu_t)] \] for all \(s\) and \(t\).

• When no confusion exists, we will drop the \(x\) as with the mean function i.e. \(\gamma(s, t)\) instead of \(\gamma_x(s, t)\)
• How can we write \(var(x_t)\) in terms of \(\gamma\)? \[ \gamma_x(t,t) = \E[(x_t - \mu_t)^2] = var(x_t) \]

Example 2.6 Autocovariance of White Noise

\(w_t\) ⬅️ white noise series

\(\gamma_w(s, t) = cov(w_s, w_t) = \text{ }?\)

Example 2.6 Autocovariance of White Noise

\(w_t\) ⬅️ white noise series

\(\gamma_w(s, t) = cov(w_s, w_t) = \begin{cases} \sigma^2_w & \text{ if } s = t\\ 0 & \text{ if } s \ne t \end{cases}\)

Example 2.8 Autocovariance of a Moving Average

Consider three point moving average \(v_t = \frac{1}{3}(w_{t-1} + w_t + w_{t+1})\)

\(\gamma_v(s, t) = cov(v_s, v_t) = \begin{cases}a & \text{ if } s = t\\ b & \text{ if } \vert s-t \vert = 1 \\c& \text{ if } \vert s-t \vert =2 \\ d & \text{ if } \vert s - t\vert > 2\end{cases}\)

• Which one of \(a, b, c, d\) is 0
• Are \(a, b, c\) the same? If not, which is largest?

Example 2.8 Autocovariance of a Moving Average

Consider three point moving average \(v_t = \frac{1}{3}(w_{t-1} + w_t + w_{t+1})\)

\(\gamma_v(s, t) = cov(v_s, v_t) = \begin{cases}\frac{3}{9}\sigma^2_w & \text{ if } s = t\\ \frac{2}{9}\sigma^2_w & \text{ if } \vert s-t \vert = 1 \\\frac{1}{9}\sigma^2_w & \text{ if } \vert s-t \vert =2 \\0 & \text{ if } \vert s - t\vert > 2\end{cases}\)

Does this equation make intuitive sense?

Example 2.9 Autocovariance of a Random Walk

\(x_t = \sum_{j = 1}^t w_j\)

\[ \gamma_x(s, t) = cov(x_s, x_t) = cov\left ( \sum_{j=1}^s w_j, \sum_{k = 1}^t w_k\right ) = \min\{s,t\}\sigma^2_w \] If you waaaaant, property 2.7 and figuring out what \(\E(w_jw_k)\) is for \(j \ne k\)

In-class R problems

R example - Moving Average

# generate white noise
n = 50
w_t <- rnorm(n, 0, 1)

## manually lag terms
w_t1 <- c(NA, w_t[1:(n-1)])
w_t2 <- c(NA, NA, w_t[1:(n-2)])

## manually compute MA(3)
v_t <- ?

## compare the vectors
ma_3 <- cbind(v_t, w_t, w_t1, w_t2, w_t3)
round(ma_3, 3)

## also compute MA(3) using stats::filter
v_t_alt <- ?
  
## plot both

R example - Moving Average

# generate white noise
n = 50
w_t <- rnorm(n, 0, 1)

## manually lag terms
w_t1 <- c(NA, w_t[1:(n-1)])
w_t2 <- c(NA, NA, w_t[1:(n-2)])
w_t3 <- c(NA, NA, NA, w_t[1:(n-3)])
## manually compute MA(3)
v_t <- (w_t + w_t1 + w_t2 + w_t3)/4

## compare the vectors
ma_3 <- cbind(v_t, w_t, w_t1, w_t2, w_t3)
round(ma_3, 3)

         v_t    w_t   w_t1   w_t2   w_t3
 [1,]     NA  1.063     NA     NA     NA
 [2,]     NA  0.150  1.063     NA     NA
 [3,]     NA -1.161  0.150  1.063     NA
 [4,] -0.227 -0.958 -1.161  0.150  1.063
 [5,] -0.619 -0.507 -0.958 -1.161  0.150
 [6,] -0.807 -0.600 -0.507 -0.958 -1.161
 [7,] -0.913 -1.587 -0.600 -0.507 -0.958
 [8,] -0.710 -0.144 -1.587 -0.600 -0.507
 [9,] -0.790 -0.827 -0.144 -1.587 -0.600
[10,] -0.460  0.717 -0.827 -0.144 -1.587
[11,]  0.041  0.419  0.717 -0.827 -0.144
[12,]  0.198  0.483  0.419  0.717 -0.827
[13,]  0.463  0.235  0.483  0.419  0.717
[14,]  0.128 -0.624  0.235  0.483  0.419
[15,] -0.186 -0.837 -0.624  0.235  0.483
[16,]  0.053  1.438 -0.837 -0.624  0.235
[17,]  0.271  1.107  1.438 -0.837 -0.624
[18,]  0.512  0.342  1.107  1.438 -0.837
[19,]  0.468 -1.014  0.342  1.107  1.438
[20,]  0.577  1.871 -1.014  0.342  1.107
[21,]  0.100 -0.802  1.871 -1.014  0.342
[22,] -0.041 -0.221 -0.802  1.871 -1.014
[23,]  0.402  0.758 -0.221 -0.802  1.871
[24,]  0.390  1.823  0.758 -0.221 -0.802
[25,]  0.661  0.282  1.823  0.758 -0.221
[26,]  0.755  0.157  0.282  1.823  0.758
[27,]  0.805  0.956  0.157  0.282  1.823
[28,]  0.850  2.003  0.956  0.157  0.282
[29,]  0.892  0.453  2.003  0.956  0.157
[30,]  0.928  0.300  0.453  2.003  0.956
[31,]  0.822  0.531  0.300  0.453  2.003
[32,]  0.790  1.877  0.531  0.300  0.453
[33,]  0.551 -0.503  1.877  0.531  0.300
[34,]  0.239 -0.950 -0.503  1.877  0.531
[35,]  0.383  1.110 -0.950 -0.503  1.877
[36,] -0.425 -1.357  1.110 -0.950 -0.503
[37,] -0.033  1.063 -1.357  1.110 -0.950
[38,] -0.151 -1.422  1.063 -1.357  1.110
[39,] -0.310  0.475 -1.422  1.063 -1.357
[40,] -0.133 -0.647  0.475 -1.422  1.063
[41,] -0.338  0.242 -0.647  0.475 -1.422
[42,] -0.002 -0.077  0.242 -0.647  0.475
[43,] -0.160 -0.159 -0.077  0.242 -0.647
[44,] -0.031 -0.129 -0.159 -0.077  0.242
[45,] -0.437 -1.383 -0.129 -0.159 -0.077
[46,]  0.237  2.620 -1.383 -0.129 -0.159
[47,] -0.023 -1.201  2.620 -1.383 -0.129
[48,]  0.182  0.690 -1.201  2.620 -1.383
[49,]  0.455 -0.290  0.690 -1.201  2.620
[50,]  0.288  1.954 -0.290  0.690 -1.201

## also compute using stats::filter
v_t_alt <- stats::filter(w_t, sides = 2, filter = rep(0.25, times = 4))

Problem 1.1

Moving Averages (Problem 1.1)

• using a method similar to the code in Example 1.9, generate 100 observations from the autoregression \[ x_t = -0.9x_{t-2} + w_t\text{, }\\ w_t\sim N(0, 1) \]
• Write down an expression for \(\phi\) for this autoregression. How is \(\phi\) different from the autoregression in Example 1.9?

Moving Averages (Problem 1.1 Part a)

• Apply the moving average filter to the autoregression data you generated \[ v_t = (x_t + x_{t-1} + x_{t-2} + x_{t-4}) \]

• Plot \(x_t\) as points and lines and \(v_t\) as a line.

Moving Averages (Problem 1.1)

library(astsa)
w = rnorm(150,0,1) # 50 extra to avoid startup problems
xa = filter(w, filter=c(0,-.9), method="recursive")[-(1:50)] # AR
va = filter(xa, rep(1,4)/4, sides=1) # moving average
tsplot(xa, main="autoregression", type = "b", pch = 16)
lines(va, col="blueviolet", lwd = 2)

Moving Averages (Problem 1.1 part b)

• Repeat the application of the MA filter but instead of starting with an autoregression, generate data \(x_t\) according to the signal plus noise model \[ x_t = 2\cos(2\pi t/4) + w_t\\ w_t \sim N(0,1) \]

Moving Averages (Problem 1.1 part b)

xb = 2*cos(2*pi*(1:100)/4) + rnorm(100,0,1) # sinusoid + noise
vb = filter(xb, rep(1,4)/4, sides=1) # moving average
tsplot(xb, main="sinusoid + noise", type = "b", pch = 16)
lines(vb, col="blueviolet", lwd = 2)

Moving Averages (Problem 1.1 part c)

• Repeat the application of the MA filter but instead of starting with an autoregression, use the Johnson and Johnson data from Lecture 1.

Moving Averages (Problem 1.1 part c)

xc = log(jj)
vc = stats::filter(xc, filter = rep(1,4)/4, sides=1, method = "convolution") # moving average
tsplot(xc, main="johnson and johnson (log scale)", type = "b", pch = 16)
lines(vc, col="blueviolet", lwd = 2)

Stationarity

A time series is stationary if

• the mean function (\(\mu_t\)) is constant and does not depend on time \(t\)
• the autocovariance function (\(\gamma(s,t)\)) depends on \(s\) and \(t\) only though their difference

Example 2.14 Stationarity of a Random Walk

Look, it’s our friend the random walk:

\[ x_t = \delta t + \sum_{j = 1}^t w_j \] Their mean function is \(\E(x_t) = 0\), and their covariance function is \(\gamma_x(s, t) = \min\{s,t\}\sigma^2_w\)

Is a random walk stationary?