Lecture 3

Author

Julia Schedler

Recap

  • Visualizing time series
  • Research questions involving time series
  • Mean and covariance functions
  • Moving average examples
  • Almost got to stationarity

Today

  • Decomposing a time series

  • Stationarity

  • Autocorrelation function

  • Time series regression

First “participation” grade

  • confirm you are good to opt in or out of the textbook, you have to do it by Oct 2 so do it on Oct 1 (tomorrow).

Lecture Template

  • Download “Lecture3Template.qmd” from Canvas
  • has some basic document structure set up to make it easier to follow along in lecture :)

Another time series model

Similar to the signal plus noise model,

\[ X_t = T_t + S_t + W_t \]

  • \(T_t\) is the trend component
  • \(S_t\) is the seasonal component
  • \(W_t\) is the error component

The r function stats::decompose will split a time series \(X_t\) into these three components.

Activity 1

Code 
library(astsa)

## use the decompose function on the jj series
jj_decomp <- ## your code here
  
## plot the decomposition
## your code here

  1. Use the decompose function on the jj series.

  2. Match the terms in the equation on the previous slide to each of the components in the chart

  3. Describe the trend.

  4. Does the bottom plot (“error”) look like white noise?

  5. Look at the documentation for the decompose function. Can you determine how the “trend” component was computed?

Activity 1 (solution)

Use Lecture3Template.qmd

Activity 2

Recall the (sinusoidal) signal plus noise model: \[ w_t \sim \text{iid } N(0, \sigma^2_w)\\ x_t = 2\cos\left (\frac{2\pi t}{50} - .6\right) + w_t \]

  1. Simulate 500 observations from the signal plus noise model
  2. Apply the decompose function. Does the error portion look like white noise?

Hint: The below code gives an error. Compare the “frequency” of the jj series. Can you figure out how to use the ts function to specify the correct frequency?

Code 
cs = 2*cos(2*pi*(1:500)/50 + .6*pi)
w  = rnorm(500,0,1)
x_t = cs + w

plot(decompose(x_t))

Activity 2 (solution)

Use Lecture3Template.qmd

Comparing “math perspective” to “data perspective”

\[ w_t \sim N(0, \sigma^2_w), t = 1, \dots, n\\ x_t = 2\cos\left (\frac{2\pi t}{50} - .6\right) + w_t \]

Code 
cs = 2*cos(2*pi*(1:500)/50 + .6*pi)
w  = rnorm(500,0,1)
tsplot(cs + w)
lines(cs, col = "blueviolet", type = "l", lwd = 4)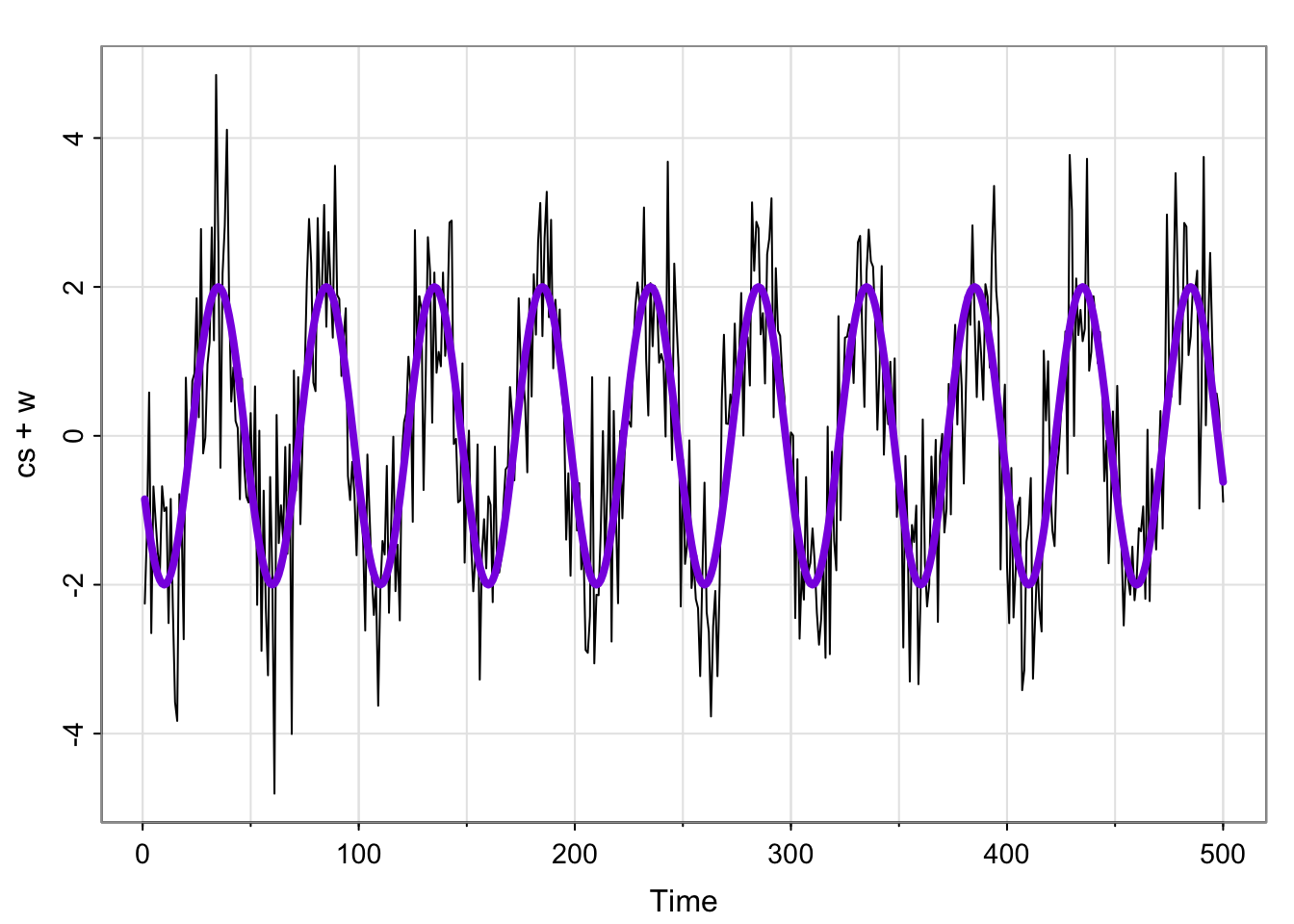

Code 
cs = 2*cos(2*pi*(1:500)/50 + .6*pi)
w  = rnorm(500,0,1)
x_t = ts(cs + w, frequency = 50)

plot(decompose(x_t))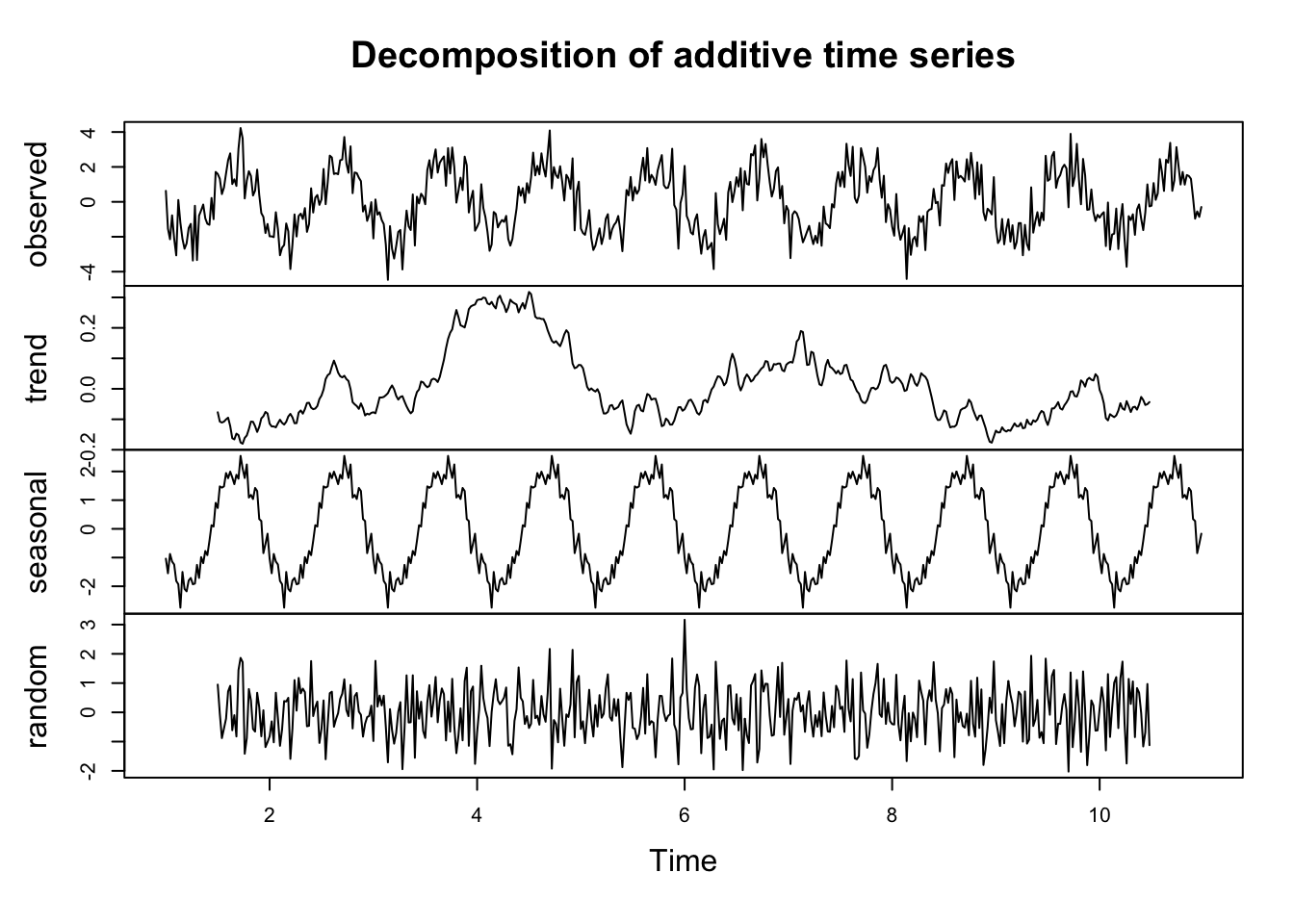

Does this function give us an estimate of the form of the mean function?

Motivating Stationarity

Review: autocovariance function

Code 
library(ggplot2)

t <- seq(1, 16, 1)
x_t <- 0.5*t 
#x <- x - mean(x)
#y <- y - mean(y)

df <- data.frame(t, x_t)

# For every row in `df`, compute a rotated normal density centered at `y` and shifted by `x`
curves <- lapply(seq_len(NROW(df)), function(i) {
  mu <- df$x_t[i]
  range <- mu + c(-1.5, 1.5)
  seq <- seq(range[1], range[2], length.out = 100)
  data.frame(
    t = -1 * dnorm(seq, mean = mu, sd = 0.5) + df$t[i],
    x_t = seq,
    grp = i
  )
})
# Combine above densities in one data.frame
curves <- do.call(rbind, curves)

new.x = seq(from = 1, to = 16, by = .1)
new.y = .5*new.x
trend_line <- data.frame(x = new.x,
                       y = new.y)
ggplot(df, aes(t, x_t)) +
  geom_point(col = "blueviolet", pch = 17) +
  #geom_line() +
  # The path draws the curve
  geom_path(data = curves, aes(group = grp)) +
  geom_line(data = trend_line, aes(x=x,y=y), col = "blueviolet") +
  lims(y = c(-2,10)) +
  scale_x_continuous(breaks = seq(1, 16, by = 1)) +
  theme_minimal() + 
  theme( # remove the vertical grid lines
           panel.grid = element_blank() ,
           # explicitly set the horizontal lines (or they will disappear too)
           panel.grid.major.x = element_line( size=.1, color="black" )) +   
  geom_rect(aes(xmin = 3.1, xmax = 4.1, ymin = 0, ymax = 4), fill = NA, col = "blue")+   
  geom_rect(aes(xmin = 7.1, xmax = 8.1, ymin = 2, ymax = 6), fill = NA, col = "magenta")
Warning: The `size` argument of `element_line()` is deprecated as of ggplot2 3.4.0.
ℹ Please use the `linewidth` argument instead.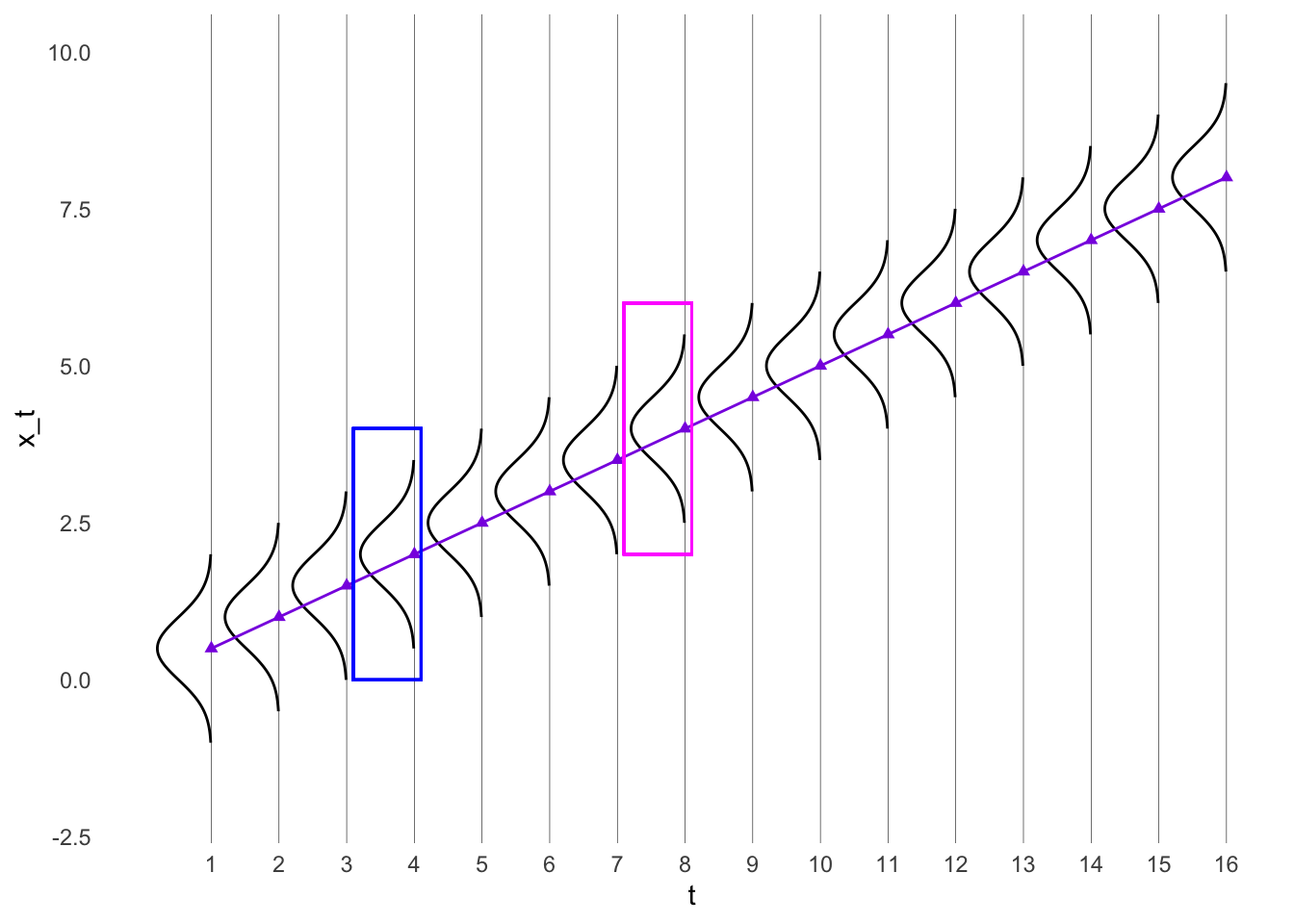

Code 
  # The polygon does the shading. We can use `oob_squish()` to set a range.
  #geom_polygon(data = curves, aes(y = scales::oob_squish(y, c(0, Inf)),group = grp))

Error covariance at different time points

Code 
# install.packages("ggplot2")
# install.packages("ggExtra")
library(ggplot2)
library(ggExtra)
set.seed(50)
x1 <- rnorm(100,x_t[4], .5)
x2 <- rnorm(100,x_t[8], .5)

x <- data.frame(x1, x2)
# Save the scatter plot in a variable
p <- ggplot(x, aes(x = x1, y = x2)) +
  geom_point() + xlim(0,6) + ylim(0,6)+ 
  geom_text(aes(x = 4, y = 2, label = "gamma(2,8) = \n cov(x_2, x_8) = 0"), size = 6) + coord_fixed() 

# Arguments for each marginal histogram
ggMarginal(p, type = "density", adjust = 2,
           xparams = list(col = "blue", fill = "blue"),
           yparams = list(col = "magenta", fill = "magenta"))
Warning in geom_text(aes(x = 4, y = 2, label = "gamma(2,8) = \n cov(x_2, x_8) = 0"), : All aesthetics have length 1, but the data has 100 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.
All aesthetics have length 1, but the data has 100 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.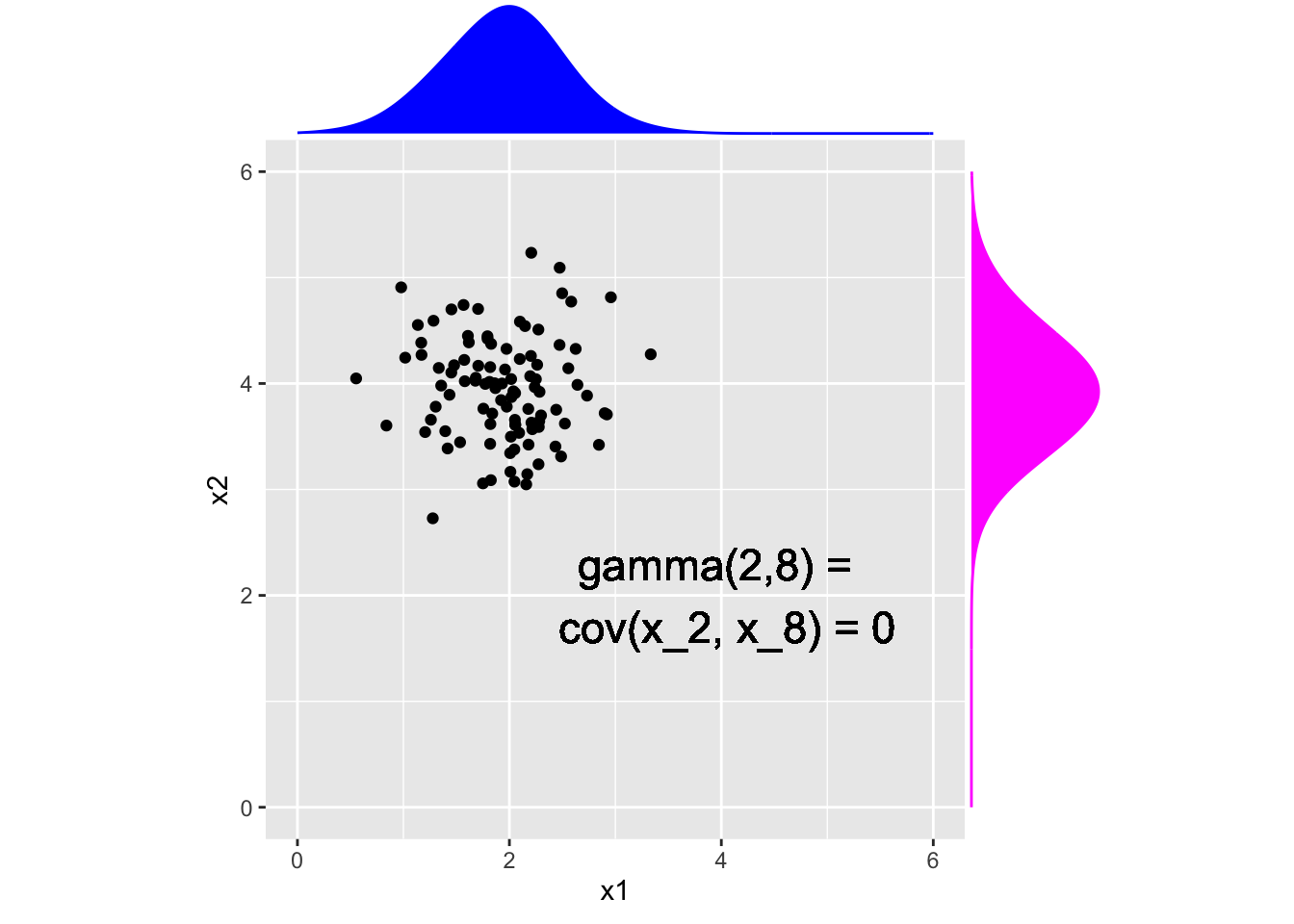

Error Covariance at Different Time Points (time dependence)

Code 
#install.packages("MASS")
library(MASS)
set.seed(100)
mu <- c(x_t[4], x_t[8])
varcov <- matrix(c(.5, .3, .3, .5), 
                 ncol = 2)
x<- mvrnorm(100, mu = mu, Sigma =varcov)
x <- data.frame(x1 = x[,1], x2 = x[,2])
# Save the scatter plot in a variable
p <- ggplot(x, aes(x = x1, y = x2)) +
  geom_point() + xlim(0,6) + ylim(0,6) + 
  geom_text(aes(x = 4, y = 2, label = "gamma(2,8) = \n cov(x_2, x_8) = 0.2"), size = 6) + coord_fixed() 

# Arguments for each marginal histogram
ggMarginal(p, type = "density", adjust = 2,
           xparams = list(col = "blue", fill = "blue"),
           yparams = list(col = "magenta", fill = "magenta"))
Warning in geom_text(aes(x = 4, y = 2, label = "gamma(2,8) = \n cov(x_2, x_8) = 0.2"), : All aesthetics have length 1, but the data has 100 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.
All aesthetics have length 1, but the data has 100 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.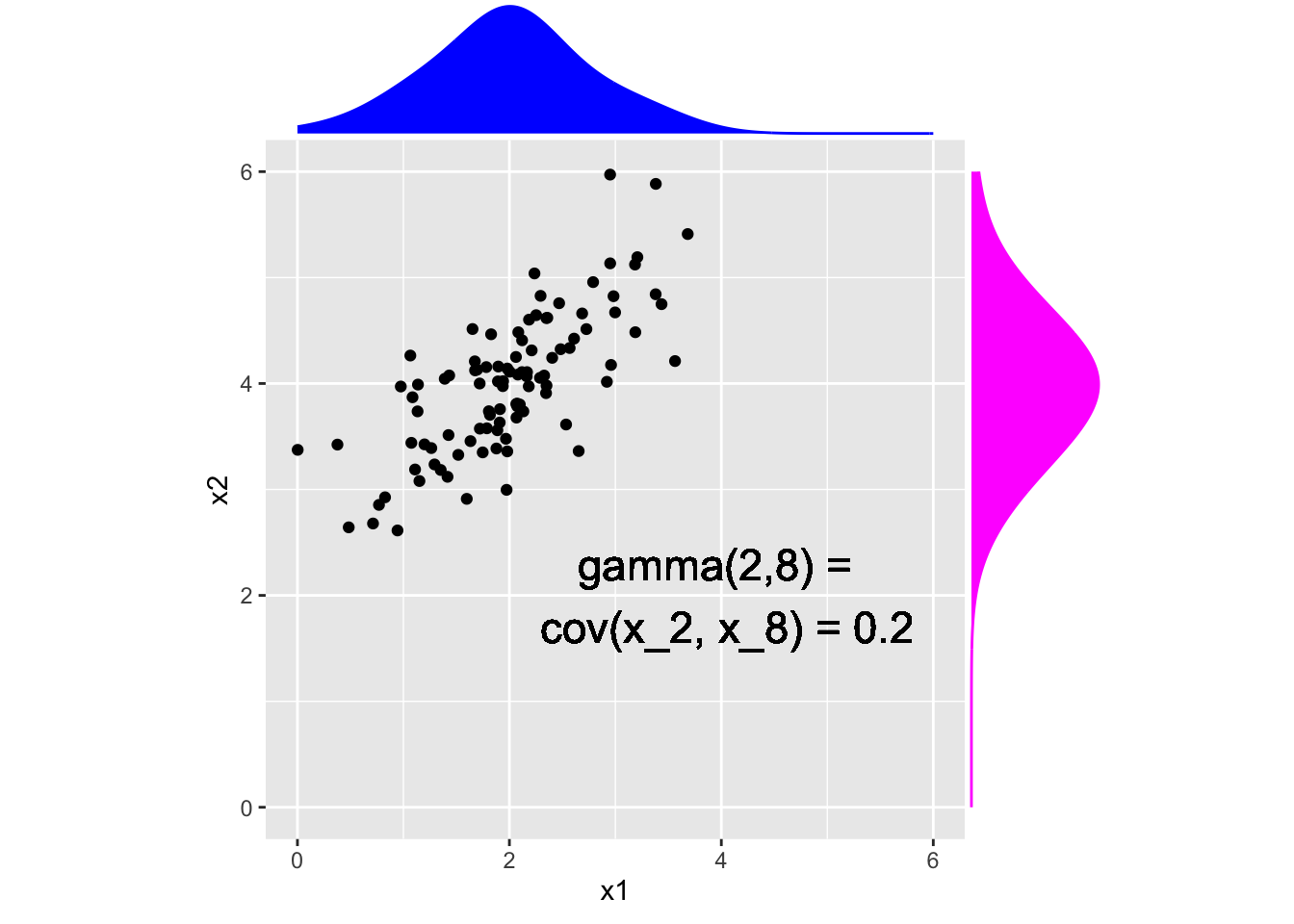

Stationarity

A time series is stationary if

  • the mean function (\(\mu_t\)) is constant and does not depend on time \(t\)
  • the autocovariance function (\(\gamma(s,t)\)) depends on \(s\) and \(t\) only though their difference

And nonstationary otherwise.

Steps to determine whether a time series \(x_t\) is stationary:

  1. Compute the mean function.
  2. Compute the autocovariance function.
  3. If both do not depend on \(t\), then \(x_t\) is stationary. Otherwise, \(x_t\) is nonstationary.

Activity 3: Example 2.14 Stationarity of a Random Walk

\[ x_t = x_{t-1} + w_t \]

Last, time, we saw that the mean function is \(\E(x_t) = 0\), and the autocovariance function is \(\gamma_x(s, t) = \min\{s,t\}\sigma^2_w\)

  1. Is \(x_t\) stationary?
  2. What if there was drift?

Activity 3 (solution)

Use Lecture3Template.qmd

\(\gamma(s,t)\) for a random walk

Code 
sigma_w <- 5 #define variance of the white noise
coords <- expand.grid(1:20, 1:20)
names(coords) <- c("s", "t") ## the coordinates represent different possible time points
coords$gamma <- pmin(coords$s, coords$t)*sigma_w


library(plotly)

Attaching package: 'plotly'
The following object is masked from 'package:MASS':

    select
The following object is masked from 'package:ggplot2':

    last_plot
The following object is masked from 'package:stats':

    filter
The following object is masked from 'package:graphics':

    layout
Code 
plot_ly(coords,
  x= ~s, y=~t, z=~gamma, 
  type = 'scatter3d', mode = "markers", size = .1)

Is white noise stationary?

  • Mean function of white noise is \(\E(w_t) = 0\)
  • Autocovariance function is \[ \gamma_w(s, t) = cov(w_s, w_t) = \begin{cases} \sigma^2_w & \text{ if } s = t\\ 0 & \text{ if } s \ne t \end{cases} \] Since neither depends on \(t\), white noise is stationary.

\(\gamma(s,t)\) for white noise

Code 
# plot the autocov's we computed last time, show on model of time series
Code 
## white noise
sigma_w <- 5 #define variance of the white noise
coords <- expand.grid(1:20, 1:20)
names(coords) <- c("s", "t") ## the coordinates represent different possible time points
coords$gamma <- 0
coords$gamma[coords[,1] == coords[,2]] <- sigma_w ## covariance is sigma_w if s = t, 0 otherwise


library(plotly)
plot_ly(coords,
  x= ~s, y=~t, z=~gamma, 
  type = 'scatter3d', mode = "markers", size = .1)

Break

Activity 4

Which of the following time series are stationary?

From Forecasting Principles and Practice Chapter 9

Activity 4 (solution)

Use Lecture3Template.qmd

Why is stationarity important?

  • In order to measure correlation between contiguous time points
  • To avoid spurious correlations in a regression setting
  • Simplifies how we can write the autocovariance and autocorrelation functions

Autocorrelation function

The autocorrelation function (acf) of a time series is: \[ \rho(s, t) = \frac{\gamma(s,t)}{\sqrt{\gamma(s,s)\gamma(t,t)}} \] i.e. the autocovariance divided by the standard deviation of the process at each time point.

Autocovariance and Autocorrelation for Stationary Time series

Since for stationary time series the autocovariance depends on \(s\) and \(t\) only through their difference, we can write the covariance as: \[ \gamma(s,t) = \gamma(h) = cov(x_{t+h}, x_t) = \E[(x_{t+h} - \mu)(x_t-\mu)] \] and the correlation as: \[ \rho(s,t) = \rho(h) = \frac{\gamma(h)}{\gamma(0)} \] \(h = s-t\) is called the lag.

Autocorrelation function of a three-point moving average

\(\gamma_v(s, t) = cov(v_s, v_t) = \begin{cases}\frac{3}{9}\sigma^2_w & \text{ if } s = t\\ \frac{2}{9}\sigma^2_w & \text{ if } \vert s-t \vert = 1 \\\frac{1}{9}\sigma^2_w & \text{ if } \vert s-t \vert =2 \\0 & \text{ if } \vert s - t\vert > 2\end{cases}\)

Since \(v\) is stationary, we can write

\(\gamma_v(h) = \begin{cases}\frac{3}{9}\sigma^2_w & \text{ if } h = 0\\ \frac{2}{9}\sigma^2_w & \text{ if } h = \pm1 \\\frac{1}{9}\sigma^2_w & \text{ if }h = \pm 2 \\0 & \text{ if } h> 2\end{cases}\)

And the autocorrelation is:

\(\rho(h) = \begin{cases}1 & \text{ if } h = 0\\ \frac{2}{3} & \text{ if } h = \pm1 \\\frac{1}{3}_w & \text{ if }h = \pm 2 \\0 & \text{ if } h> 2\end{cases}\)

Autocorrelation function of a three-point moving average

In R, we can plot \(\rho(h)\)

Code 
ACF = c(0,0,0,1,2,3,2,1,0,0,0)/3
LAG = -5:5
tsplot(LAG, ACF, type="h", lwd=3, xlab="LAG")   
abline(h=0)
points(LAG[-(4:8)], ACF[-(4:8)], pch=20)
axis(1, at=seq(-5, 5, by=2))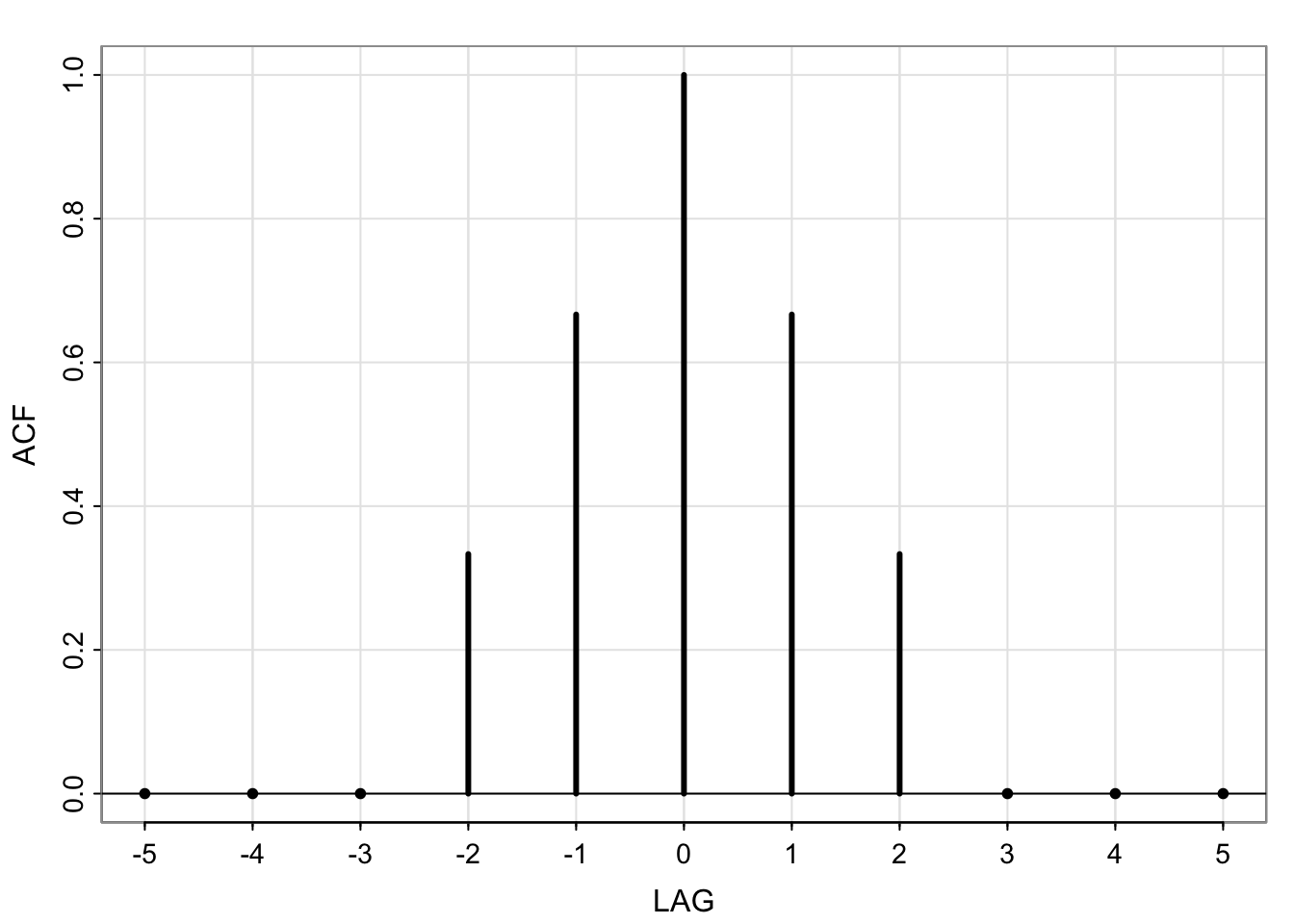

Activity 5

  1. Predict what the acf will look like for the ar(1) process?
  2. Simulate an ar(1) process and compute the acf. Were you correct?
  3. What is the lag 0 autocorrelation? Explain why its value makes sense.
Code 
# simulate from an ar(1)

# use acf() function to plot acf

# save output of acf and inspect

Activity 5 (solution)

Use Lecture3Template.qmd

Questions on the quiz?

Activity 6 (Problem 2.3)

When smoothing time series data, it is sometimes advantageous to give decreasing amounts of weights to values farther away from the center. Consider the simple two-sided moving average smoother of the form: \[ v_t = \frac{1}{4}(w_{t-1} + w_t + w_{t+1}) \] Where \(w_t\) are white noise. The autocovariance as a function of \(h\) is: \[\gamma_v(s, t) = cov(v_s, v_t) = \begin{cases}\frac{6}{16}\sigma^2_w & \text{ if } h = 0\\ \frac{4}{16}\sigma^2_w & \text{ if } h = \pm 1 \\\frac{1}{16}\sigma^2_w & \text{ if } h = \pm 2 \\0 & \text{ if } h> 2\end{cases}\] 1. Compare to the autocovariance equation for the unweighted 3 point moving average from Lecture 2. Comment on the differences.

  1. Write down the autocorrelation function.

Activity 6 (solution)

Use Lecture3Template.qmd ## Activity 7 Recall the decomposition of the Johnson and Johnson quarterly earnings.

Code 
plot(decompose(jj)) ## plot decomposition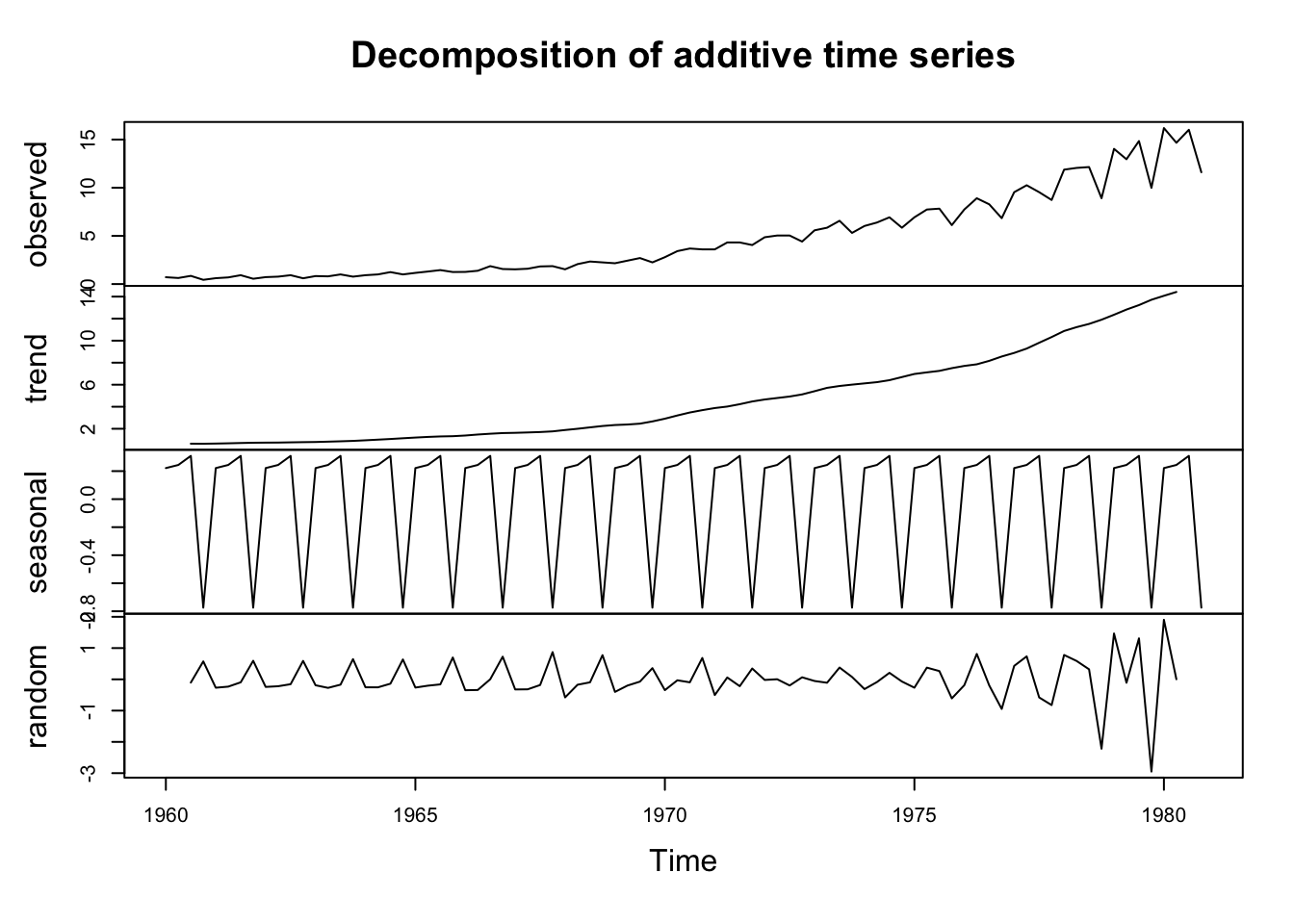

  1. Is the series stationary?
  2. Does the acf of the random component look like white noise?

Activity 7 (solution)

Use Lecture3Template.qmd

Coming up:

  • Assignment 1 due at midnight
  • Assignment 2 posted later
  • Part of this will be involve “reading” the textbook! (collecting data on how you feel about the math)
  • Next Lecture:
    • Regression with time
    • Cross-correlation
    • Inducing stationarity