Lecture 8 (with solutions)

Author

Julia Schedler

Recall the SOI data

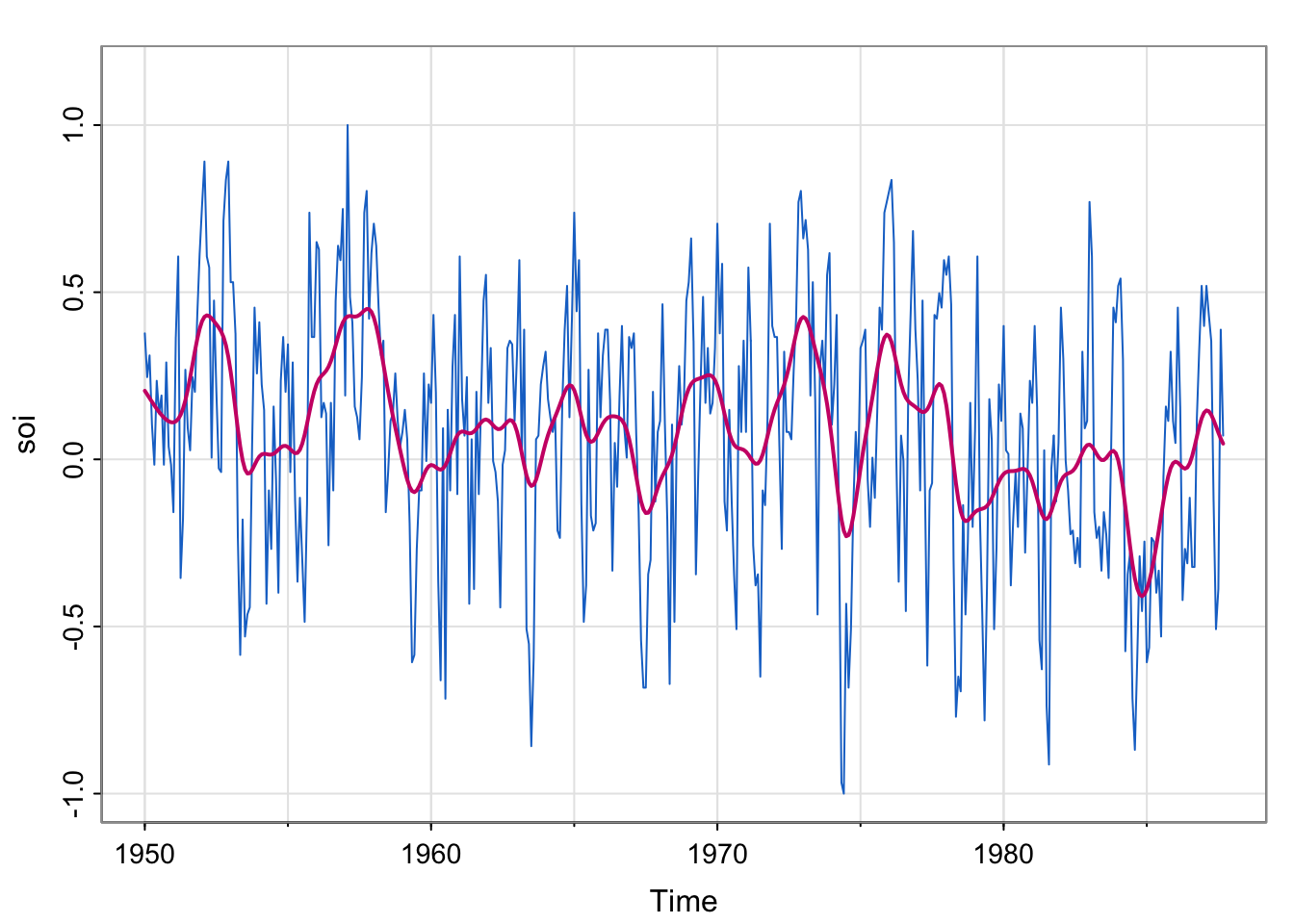
SOI : Southern Oscillation Index, a climate variable. Low values correspond to warming and high values correspond to cooling. Plotting a smoother estimate (say, kernel) reveals the El Niño cycle. (we explored this in Lecture 6).

Code 
library(astsa)
tsplot(soi, col=4, ylim = c(-1, 1.15))
lines(ksmooth(time(soi), soi, "normal", bandwidth=1), lwd=2, col=6)

The autocorrelation function

Code 
soi_ksmooth <- ksmooth(time(soi), soi, "normal", bandwidth=1)
detrended <- soi-soi_ksmooth$y

## acf of soi/ detrended soi
par(mfrow = c(2,1))
acf1(soi)
 [1]  0.60  0.37  0.21  0.05 -0.11 -0.19 -0.18 -0.10  0.05  0.22  0.36  0.41
[13]  0.31  0.10 -0.06 -0.17 -0.29 -0.37 -0.32 -0.19 -0.04  0.15  0.31  0.35
[25]  0.25  0.10 -0.03 -0.16 -0.28 -0.37 -0.32 -0.16 -0.02  0.17  0.33  0.39
[37]  0.30  0.16  0.00 -0.13 -0.24 -0.27 -0.25 -0.13  0.06  0.21  0.38  0.40
Code 
acf1(detrended)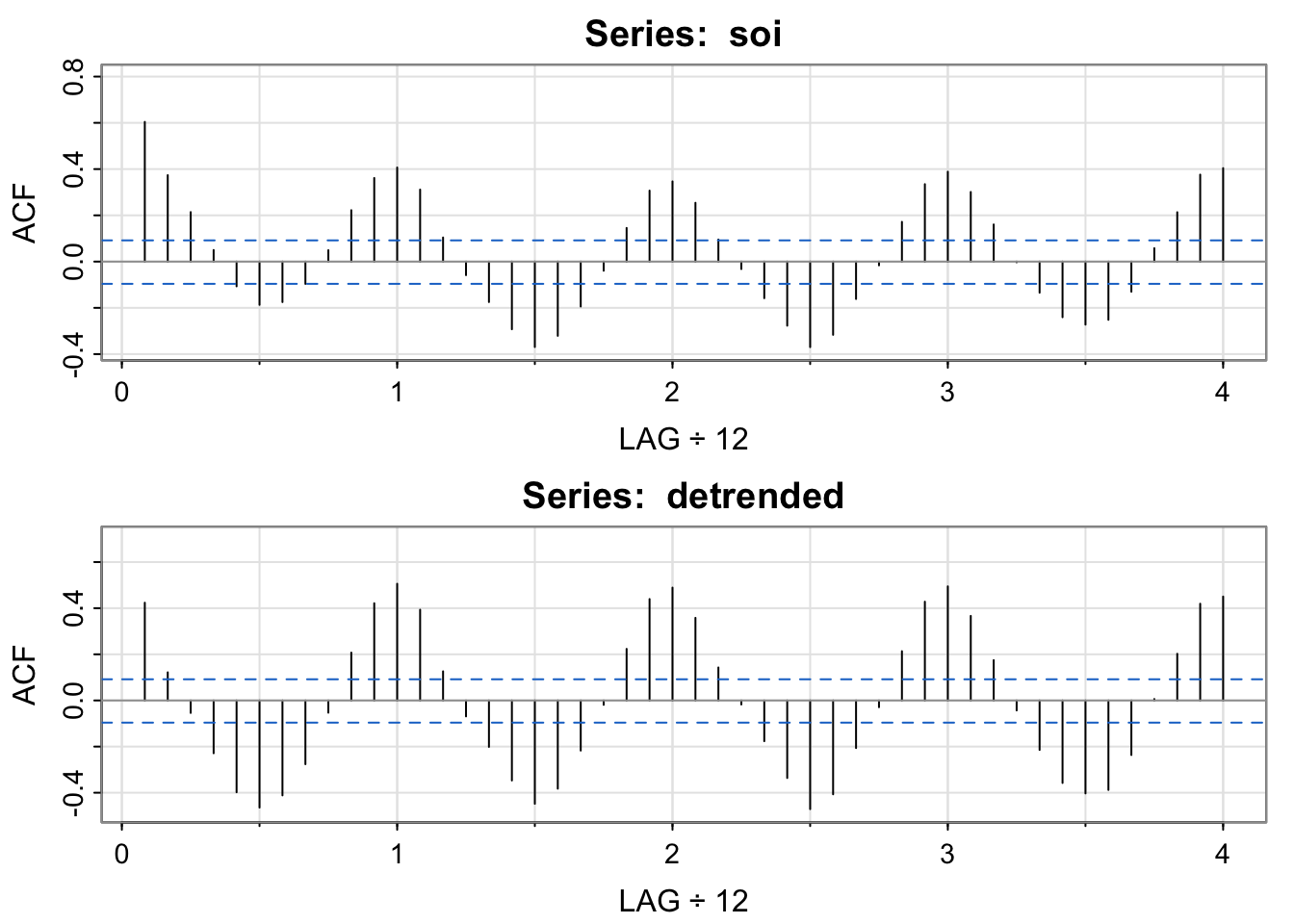

 [1]  0.42  0.12 -0.05 -0.23 -0.40 -0.46 -0.41 -0.28 -0.05  0.21  0.42  0.51
[13]  0.39  0.13 -0.07 -0.20 -0.35 -0.45 -0.38 -0.22 -0.02  0.22  0.44  0.49
[25]  0.36  0.14 -0.02 -0.18 -0.34 -0.47 -0.41 -0.21 -0.03  0.21  0.43  0.49
[37]  0.37  0.17 -0.04 -0.21 -0.36 -0.40 -0.39 -0.24  0.01  0.20  0.42  0.45
Code 
par(mfrow = c(1,1))

Note the clear seasonal pattern– it’s yearly (monthly frequency divided by 12 means a lag of 1 is a year). Also, values +/-1 year apart have nearly identical correlation structure to those +/- 2 years apart, and so on (the heights of the “bumps” are about the same. I’m showing the detrended acf to emphasize that once we have “detrended” out the El Niño pattern, we still see an annual pattern.

The pattern in the detrended acf might be called “residual temporal structure”, specifically, a seasonal pattern.

Activity 1 (Example 3.13)

Code 
library(astsa)
lag1.plot(soi, 12, col=4, cex=1)      # Figure 3.10

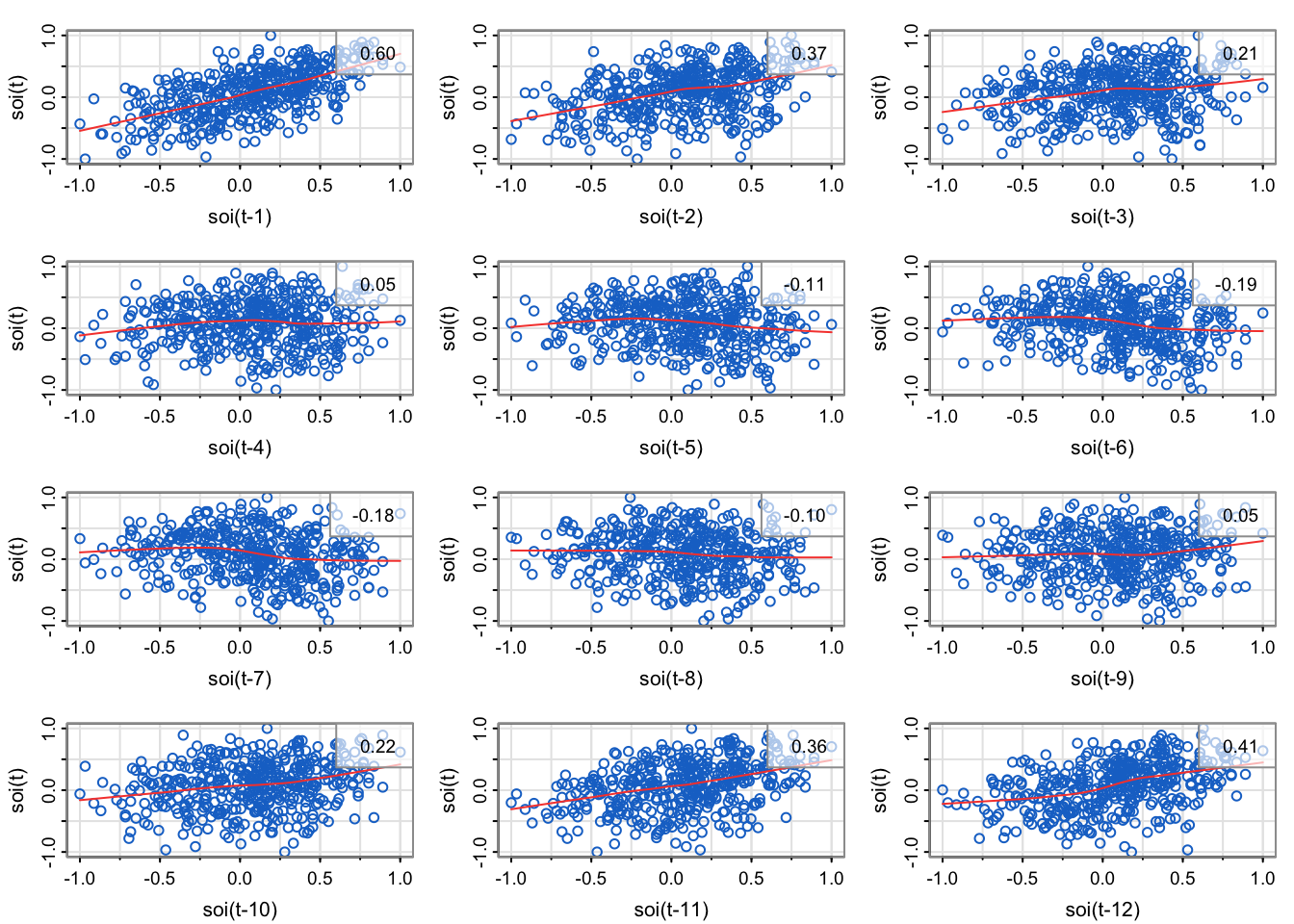
  1. Explain how the scatterplots below relate to the sample autocorrelation function of soi.

  2. Do the lagplots/loess trend estimates suggest that sample autocorrelation is a meaningful measurement for the temporal lag relationships?

  1. Is all the information in the acf represented in the scatterplot matrix of lagplots?

Activity 1 Solutions

Code 
library(astsa)
lag1.plot(soi, 12, col=4, cex=1)      # Figure 3.10

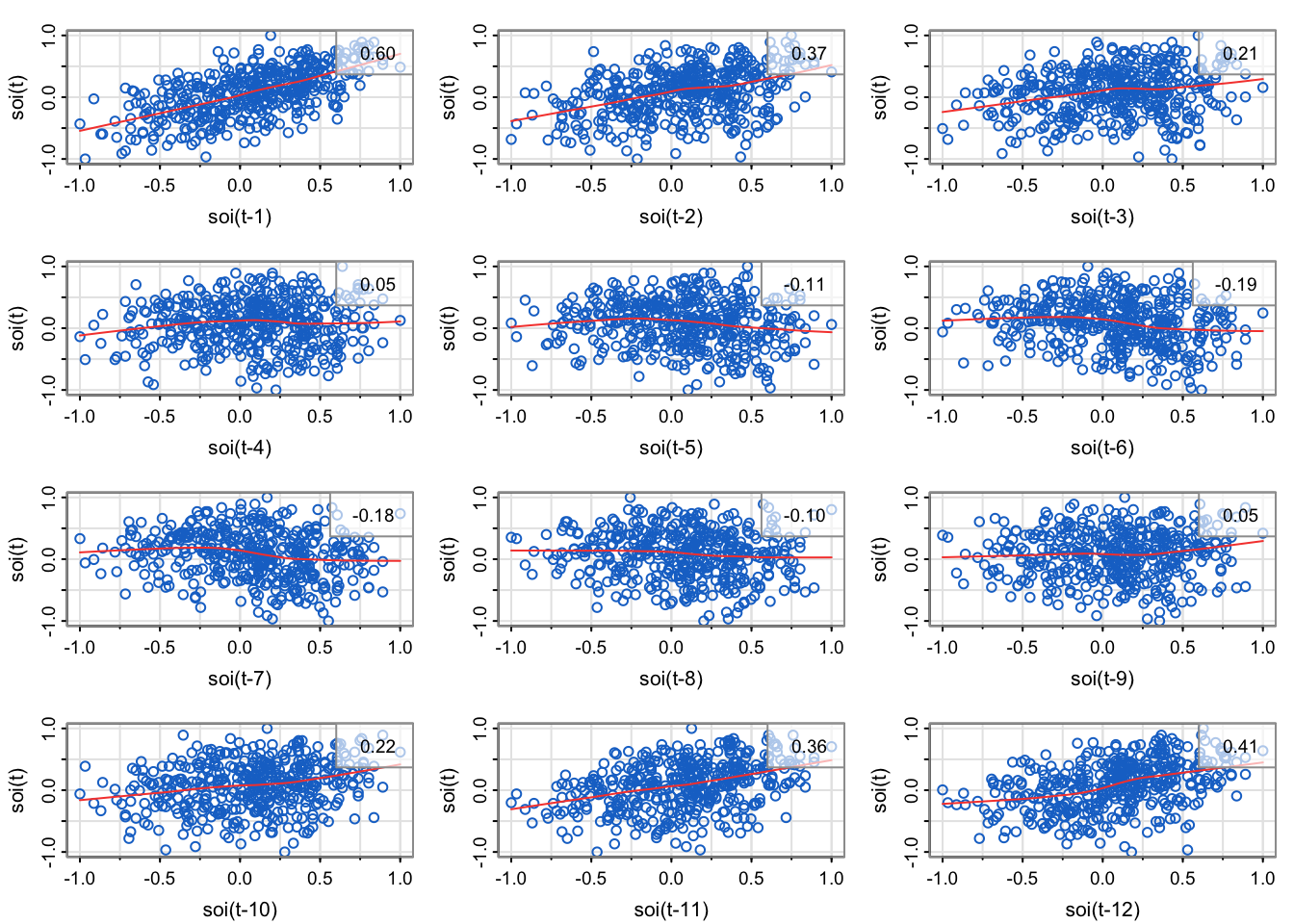
  1. Explain how the scatterplots below relate to the sample autocorrelation function of soi.

    The sample correlation in the upper right corner of each of the scatterplots match the height of the bar for the corresponding lag.

    • The plot in the upper left is the lag1 scatterplot (soi(t) vs. soi(t-1)). The correlation is 0.6, which is the height of the bar for lag 1 (0.08 on x-axis) is in the acf.

    • The plot in the middle left is the lag2 scatterplot (soi(t) vs. soi(t-2)). The correlation is 0.37, which is the height of the bar for lag 2 (0.17 on the x-axis) is in the acf.

    • …

    • the third row, first column is the lag7 scatterplot (soi(t) vs. soi(t-7)). The correlation is -0.18, which is the height of the bar for lag 7 (0.58 on x-axis) is in the acf.

    • …

    • The plot in the upper left is the lag11 scatterplot (soi(t) vs. soi(t-11)). The correlation is 0.36, which is the height of the bar for lag 11 (.92 on x-axis) is in the acf.

    • The plot in the middle left is the lag12 scatterplot (soi(t) vs. soi(t-12)). The correlation is 0.41, which is the height of the bar for lag 12 (1 on x-axis) is in the acf.

  2. Do the lagplots/loess trend estimates suggest that sample autocorrelation is a meaningful measurement for the temporal lag relationships?

Note that loess is a method for estimating a trend between any two variables (last lecture, one variable was deterministic time) that can allow for nonlinear relationships. Most of the loess fits look fairly linear, meaning that the autocorrelation is meaningful (since correlation is a linear measurement of strength, but we can compute correlation for any two vectors regardless of how inappropriate it is).

  1. Is all the information in the acf represented in the scatterplot matrix of lagplots?

In an empirical sense, no. We would need to compute the correlation of lags 13, 14, … 4*12 = 48, since that’s how far the x-axis goes on the sample autocorrelation estimate plotted by the acf1 function.

In a statistical sense, yes. It seems like the cyclical pattern is very stable (no drop off at later lags), so we could probably represent all the temporal structure with a sinusoid based on the month:

Code 
month <- seq(from = 0, to = 2*pi, by = 2*pi/12)
sinusoid <- cos(month)
plot(1:13, sinusoid, xlab = "\'month\'", ylab = "cos(\"month\")")
abline(h = 0)

Then if we repeat that four times:

Code 
month <- seq(from = 0, to = 8*pi, by = 2*pi/12)
sinusoid <- cos(month)
plot(1:49, sinusoid, xlab = "Month (#)", ylab = "cos(\"month\")")
abline(h = 0)

… and add vertical lines…

Code 
month <- seq(from = 0, to = 8*pi, by = 2*pi/12)
sinusoid <- cos(month)
plot(1:49, sinusoid, xlab = "\'month\'", ylab = "cos(\"month\")")
abline(h = 0)
segments(x0 = 1:49, y0= 0, y1 = sinusoid)

… it starts to look like the acf– the scaling is just off.

Code 
par(mfrow = c(2,1))
acf1(soi)
 [1]  0.60  0.37  0.21  0.05 -0.11 -0.19 -0.18 -0.10  0.05  0.22  0.36  0.41
[13]  0.31  0.10 -0.06 -0.17 -0.29 -0.37 -0.32 -0.19 -0.04  0.15  0.31  0.35
[25]  0.25  0.10 -0.03 -0.16 -0.28 -0.37 -0.32 -0.16 -0.02  0.17  0.33  0.39
[37]  0.30  0.16  0.00 -0.13 -0.24 -0.27 -0.25 -0.13  0.06  0.21  0.38  0.40
Code 
plot(1:49, sinusoid, xlab = "\'month\'", ylab = "cos(\"month\")")
abline(h = 0)
segments(x0 = 1:49, y0= 0, y1 = sinusoid)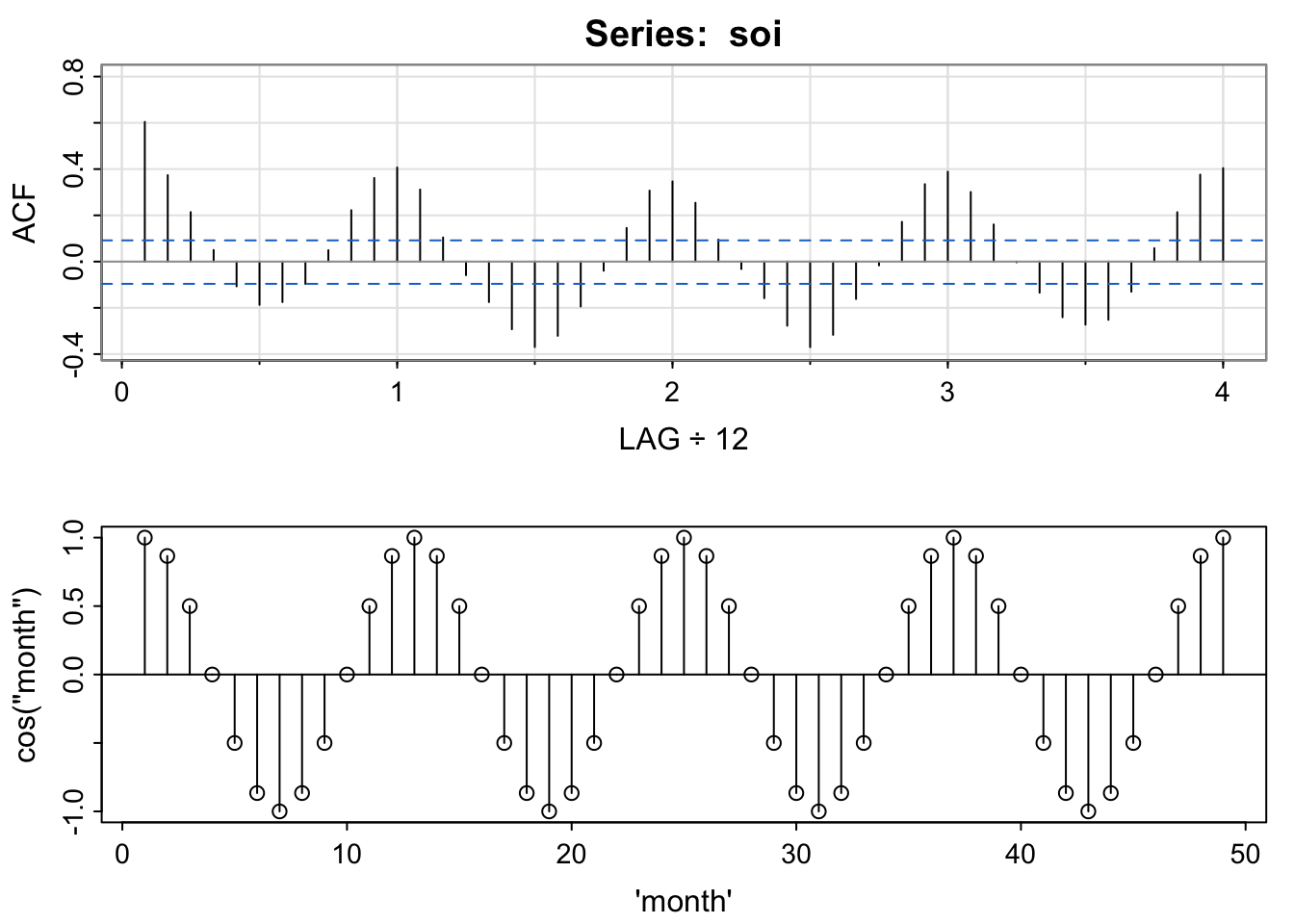

Code 
par(mfrow = c(1,1))

This is explored in chapters 6 and 7 (possible end of quarter topic).

Activity 2 (sort of Example 3.15)

Code 
set.seed(807) # so you can reproduce these results
n <- length(soi)
x  = 0.5*cos(2*pi*1:n/12) + rnorm(n,0,.25)



z1 = cos(2*pi*1:n/12)
z2 = sin(2*pi*1:n/12)
summary(fit <- lm(x~ 0 + z1 + z2)) # zero to exclude intercept
## 
## Call:
## lm(formula = x ~ 0 + z1 + z2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.70187 -0.16132  0.00053  0.15572  0.62818 
## 
## Coefficients:
##     Estimate Std. Error t value Pr(>|t|)    
## z1  0.494705   0.015859  31.194   <2e-16 ***
## z2 -0.001529   0.015824  -0.097    0.923    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2384 on 451 degrees of freedom
## Multiple R-squared:  0.6833, Adjusted R-squared:  0.6819 
## F-statistic: 486.5 on 2 and 451 DF,  p-value: < 2.2e-16
par(mfrow=c(2,1))
tsplot(x, col=4)
tsplot(x, ylab=expression(hat(x)), col=astsa.col(4, .5))
lines(fitted(fit), col=2, lwd=2)

Code 
par(mfrow=c(1,1))
acf(x)

Code 
acf(resid(fit))

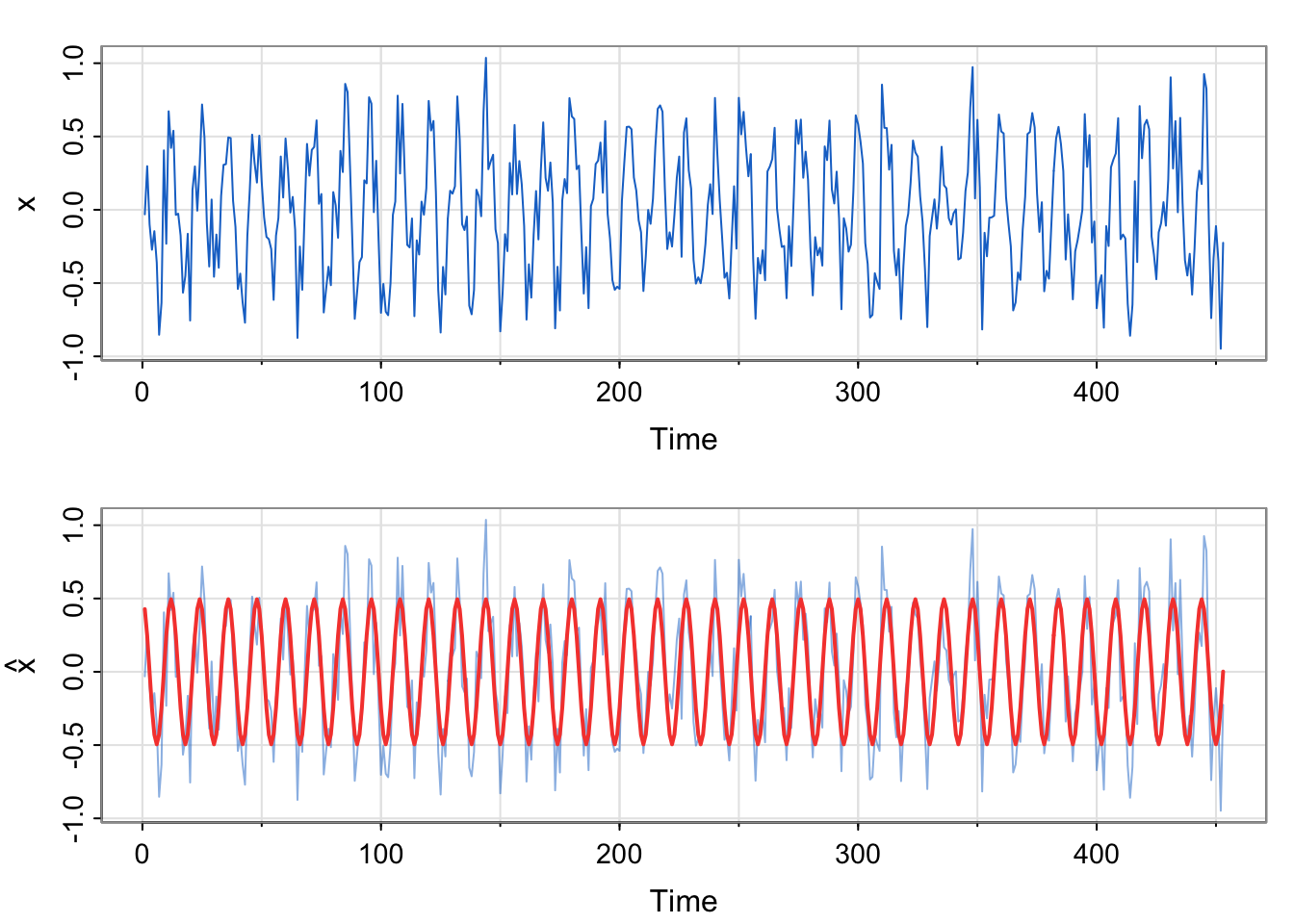
  1. How does the simulated series x relate to the previous example?
  2. What is the estimated equation for the red line?
  3. Is it surprising that the red line appears to fit the simulated series so well?
  4. Compare the autocorrelation function of soi to the autocorrelation function of the simulated series.

Activity 2 Solutions (sort of Example 3.15)

Code 
set.seed(807) # so you can reproduce these results
n <- length(soi)
x  = 0.5*cos(2*pi*1:n/12) + rnorm(n,0,.25)



z1 = cos(2*pi*1:n/12)
z2 = sin(2*pi*1:n/12)
summary(fit <- lm(x~ 0 + z1 + z2)) # zero to exclude intercept
## 
## Call:
## lm(formula = x ~ 0 + z1 + z2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.70187 -0.16132  0.00053  0.15572  0.62818 
## 
## Coefficients:
##     Estimate Std. Error t value Pr(>|t|)    
## z1  0.494705   0.015859  31.194   <2e-16 ***
## z2 -0.001529   0.015824  -0.097    0.923    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2384 on 451 degrees of freedom
## Multiple R-squared:  0.6833, Adjusted R-squared:  0.6819 
## F-statistic: 486.5 on 2 and 451 DF,  p-value: < 2.2e-16
par(mfrow=c(2,1))
tsplot(x, col=4)
tsplot(x, ylab=expression(hat(x)), col=astsa.col(4, .5))
lines(fitted(fit), col=2, lwd=2)

Code 
par(mfrow=c(1,1))
acf(x)

Code 
acf(resid(fit))

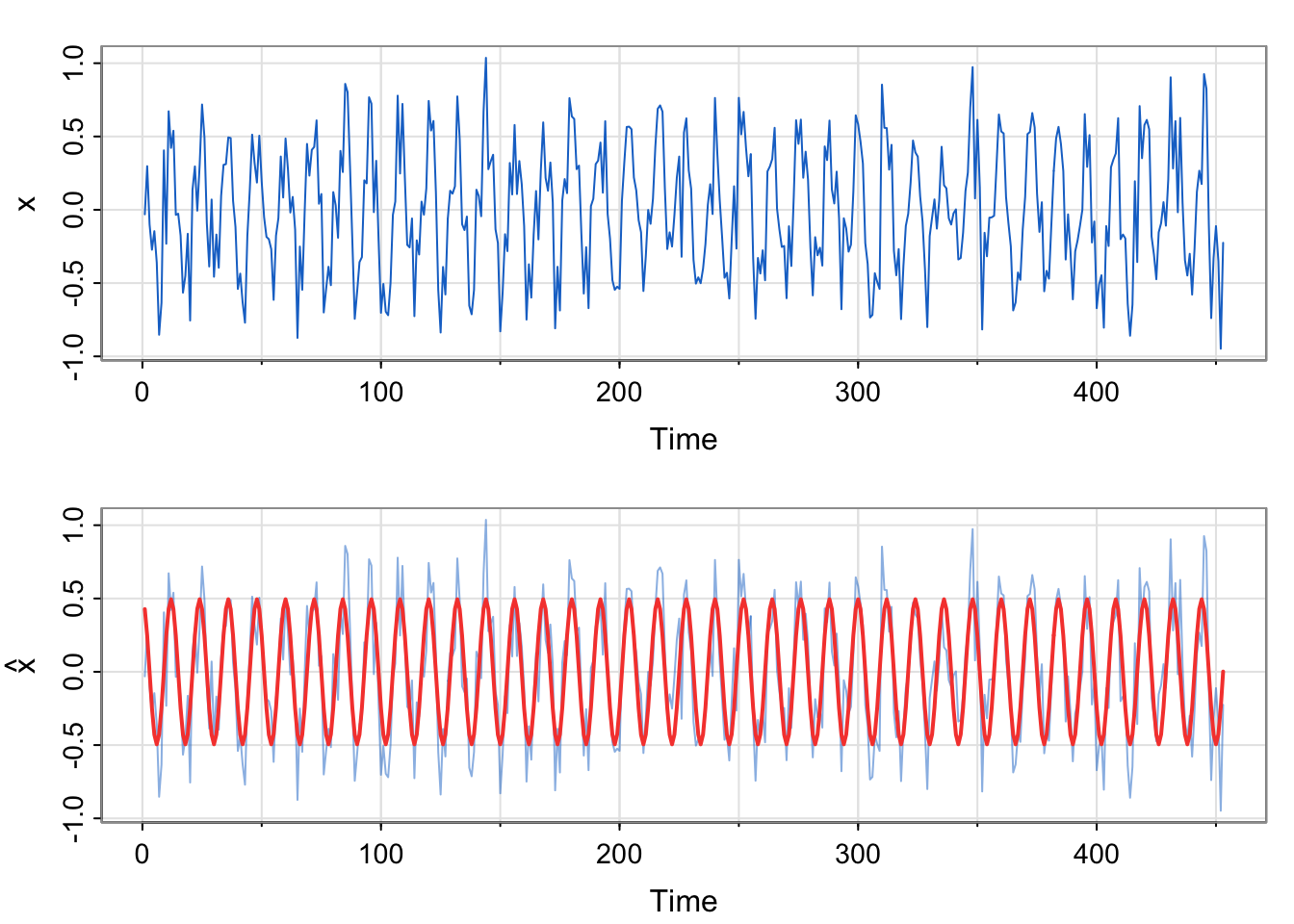
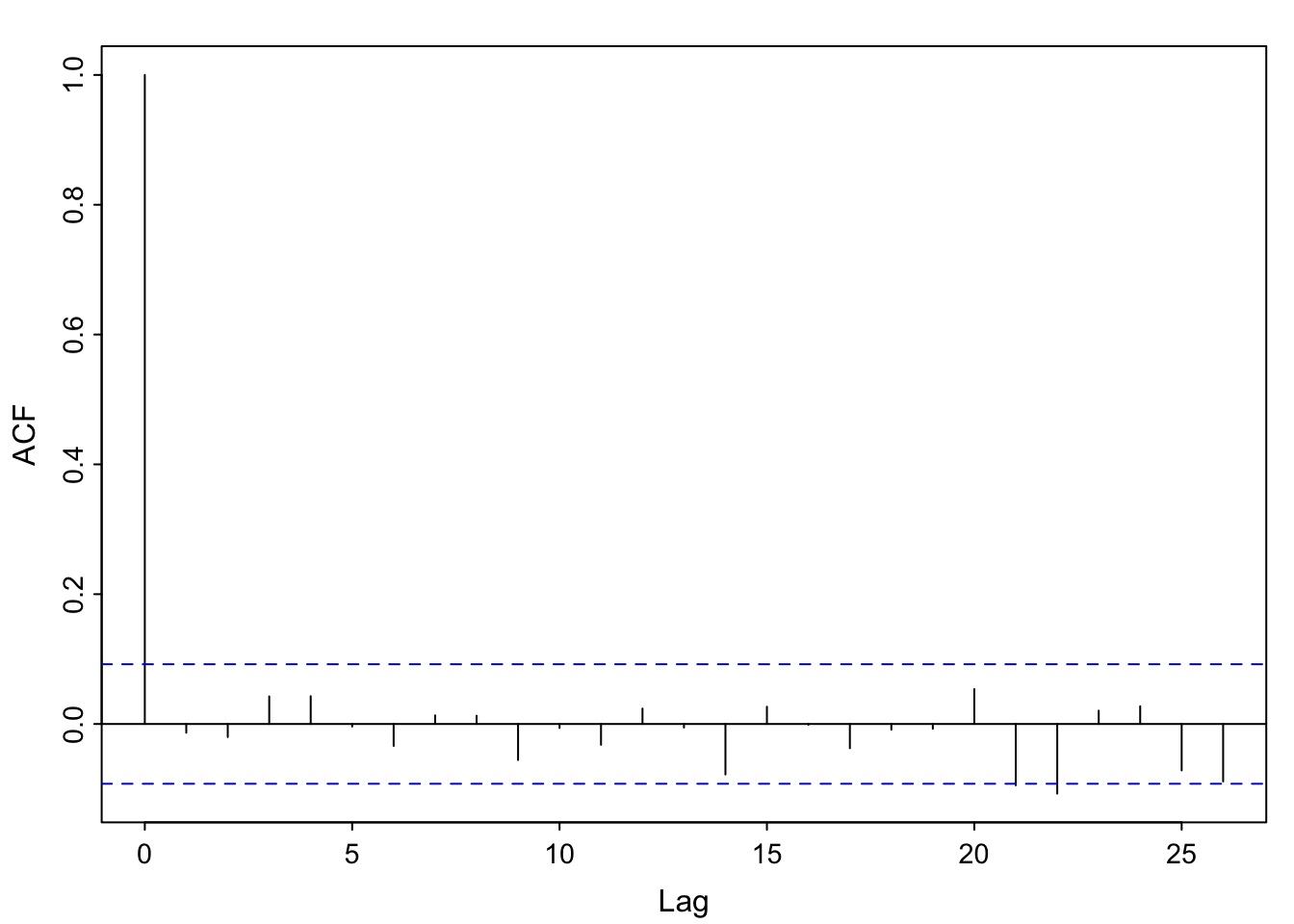
  1. How does the simulated series x relate to the previous example?

We commented that the residual temporal structure is seasonal and could be modeled by a sinusoid. Since the correlation appears to start at a high point, then decrease and reach a maximum at 1 (12 months), we choose a cosine over a sine. Here, we are simulating seasonal data, not analyzing the soi data. We do generate the same number of observations as a

  1. What is the estimated equation for the red line?

\[ \hat{x} = 0.495\cos \left (\frac{2\pi t}{12} \right) -0.002\sin \left (\frac{2\pi t}{12} \right) \]

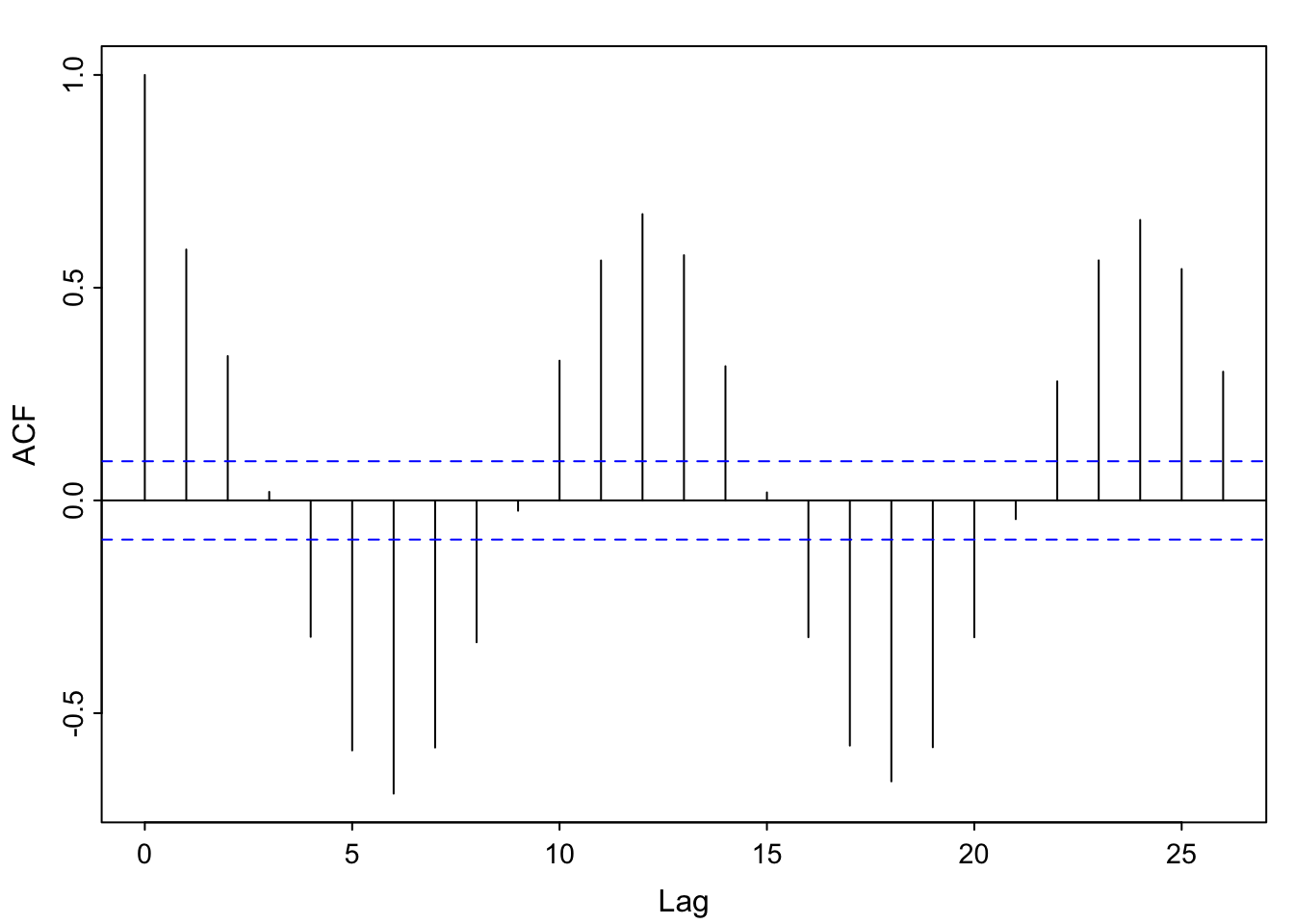
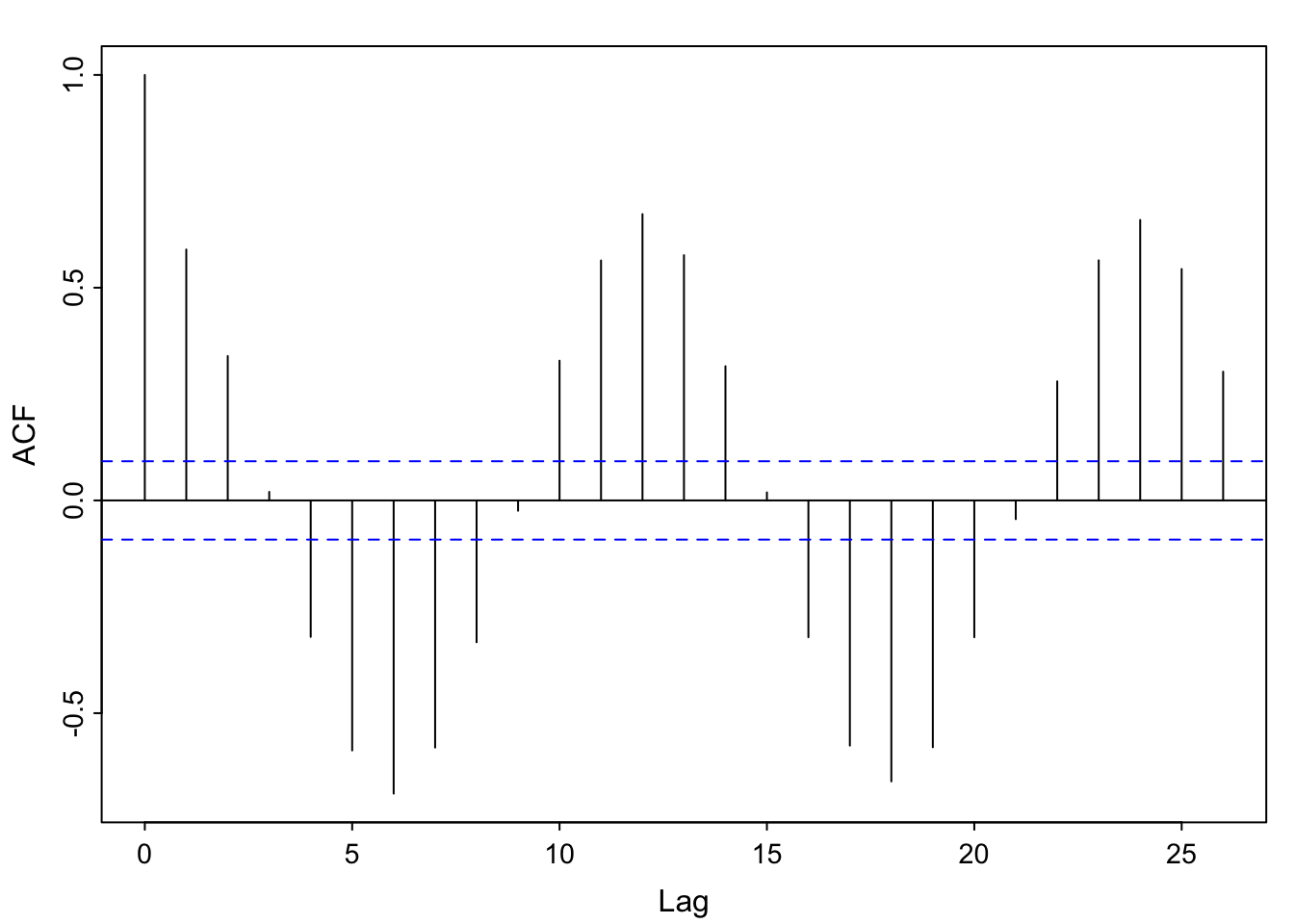
  1. Is it surprising that the red line appears to fit the simulated series so well?

No. The estimated equation weights the sine term as essentially 0, and the cosine term near 0.5. The model was generated using \(0.5\cos \left (\frac{2\pi t}{12} \right)\) for the trend component. Additionally, the acf of the residuals looks like white noise, which is what we simulated (with a smaller standard deviation to mimic the range of the soi data, though).

  1. Compare the autocorrelation function of soi to the autocorrelation function of the simulated series.

They look very similar.

Activity 3 (kinda Example 3.15)

Code 
z1 = cos(2*pi*1:n/12)
z2 = sin(2*pi*1:n/12)
summary(fit <- lm(soi~ 0 + z1 + z2)) # zero to exclude intercept
## 
## Call:
## lm(formula = soi ~ 0 + z1 + z2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.91474 -0.13174  0.08774  0.31774  0.81148 
## 
## Coefficients:
##    Estimate Std. Error t value Pr(>|t|)    
## z1  0.31292    0.02118  14.775  < 2e-16 ***
## z2  0.07348    0.02113   3.477 0.000556 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3184 on 451 degrees of freedom
## Multiple R-squared:  0.3385, Adjusted R-squared:  0.3356 
## F-statistic: 115.4 on 2 and 451 DF,  p-value: < 2.2e-16
par(mfrow=c(2,1))
tsplot(ts(soi), col=4)
tsplot(ts(soi), ylab=expression(hat(soi)), col=astsa.col(4, .5))
lines(fitted(fit), col=2, lwd=2)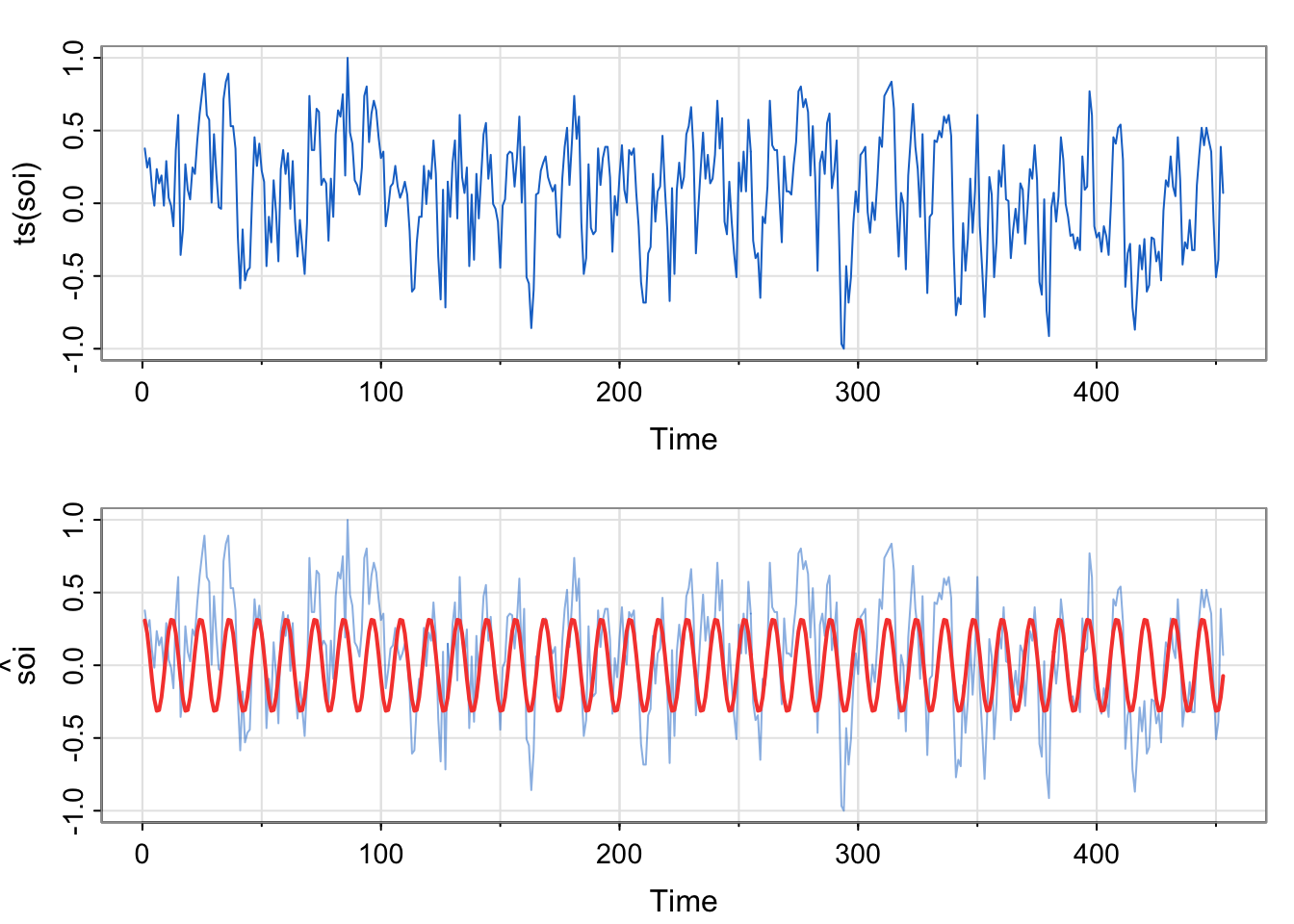

Code 
par(mfrow=c(1,1))
acf1(ts(resid(fit),freq = 12))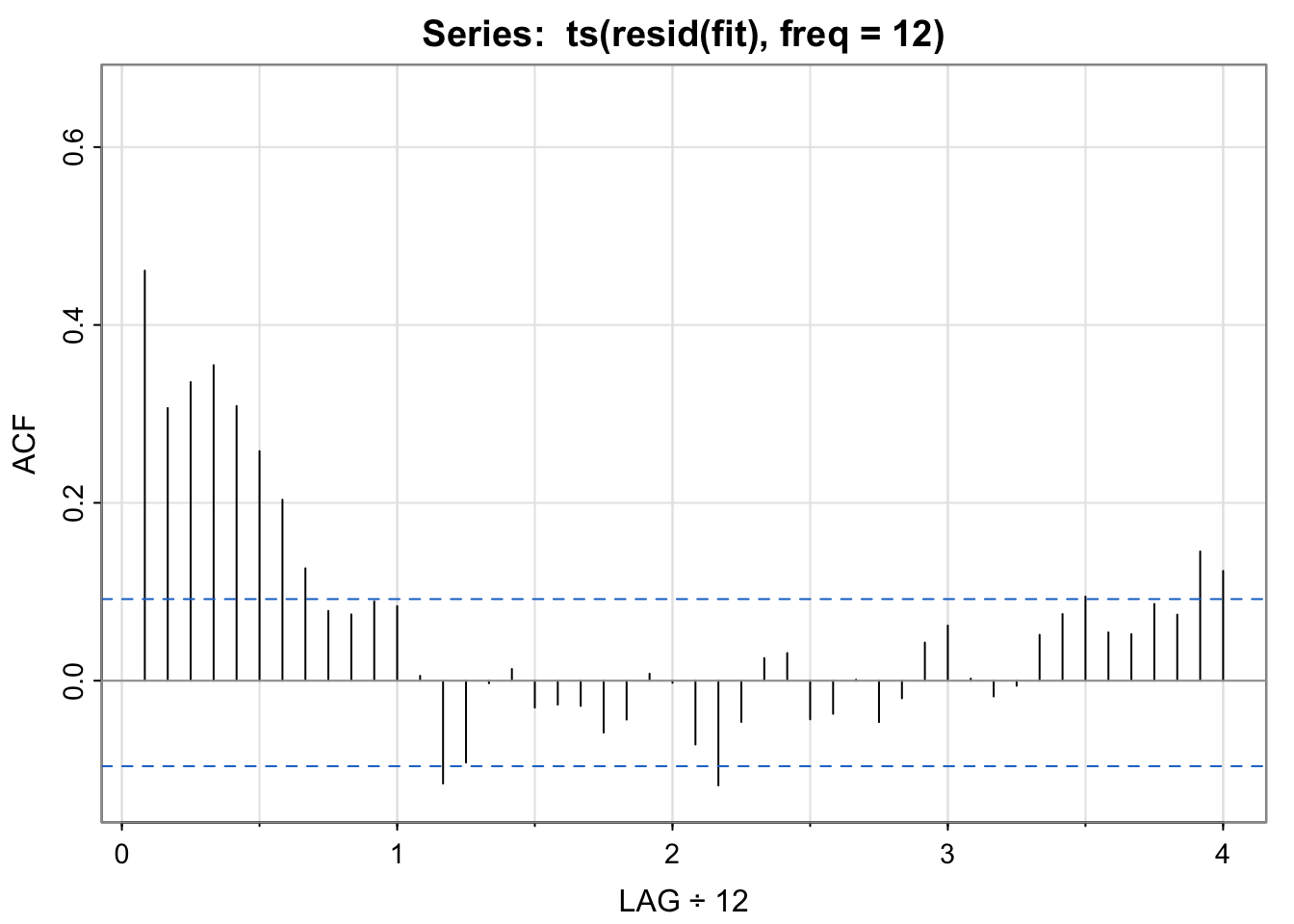

##  [1]  0.46  0.31  0.34  0.35  0.31  0.26  0.20  0.13  0.08  0.07  0.09  0.08
## [13]  0.01 -0.12 -0.09  0.00  0.01 -0.03 -0.03 -0.03 -0.06 -0.04  0.01  0.00
## [25] -0.07 -0.12 -0.05  0.03  0.03 -0.04 -0.04  0.00 -0.05 -0.02  0.04  0.06
## [37]  0.00 -0.02 -0.01  0.05  0.07  0.09  0.05  0.05  0.09  0.07  0.15  0.12
  1. What’s the difference between the model estimated in fit above vs. in Activity 2?
  2. What is the equation of the estimated seasonal trend?
  3. Does the temporal structure in soi appear to be captured by the seasonal model?
  4. Why convert to a time series before plotting the sample acf?

Activity 3 Solutions (kinda Example 3.15)

Code 
z1 = cos(2*pi*1:n/12)
z2 = sin(2*pi*1:n/12)
soi_fit <-lm(soi~  z1 + z2)
summary(soi_fit) # zero to exclude intercept
## 
## Call:
## lm(formula = soi ~ z1 + z2)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.9967 -0.2122  0.0053  0.2353  0.7295 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.08146    0.01448   5.627 3.23e-08 ***
## z1           0.31378    0.02050  15.310  < 2e-16 ***
## z2           0.07299    0.02045   3.569 0.000396 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3081 on 450 degrees of freedom
## Multiple R-squared:  0.3549, Adjusted R-squared:  0.352 
## F-statistic: 123.8 on 2 and 450 DF,  p-value: < 2.2e-16
par(mfrow=c(2,1))
tsplot(ts(soi), col=4)
tsplot(ts(soi), ylab=expression(hat(x)), col=astsa.col(4, .5))
lines(soi_fit$fitted.values, col=2, lwd=2)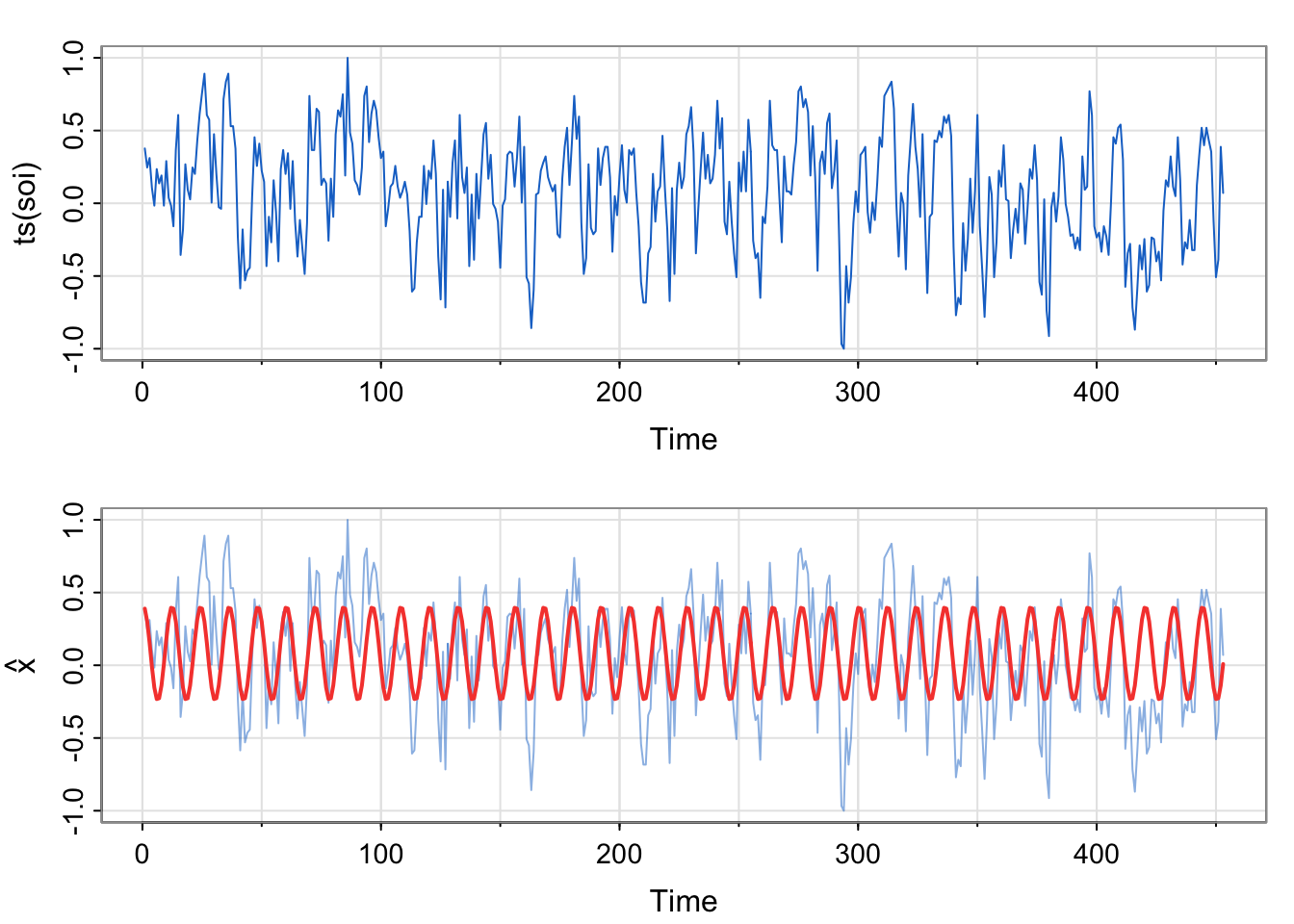

Code 
par(mfrow=c(1,1))
acf1(ts(resid(fit),freq = 12))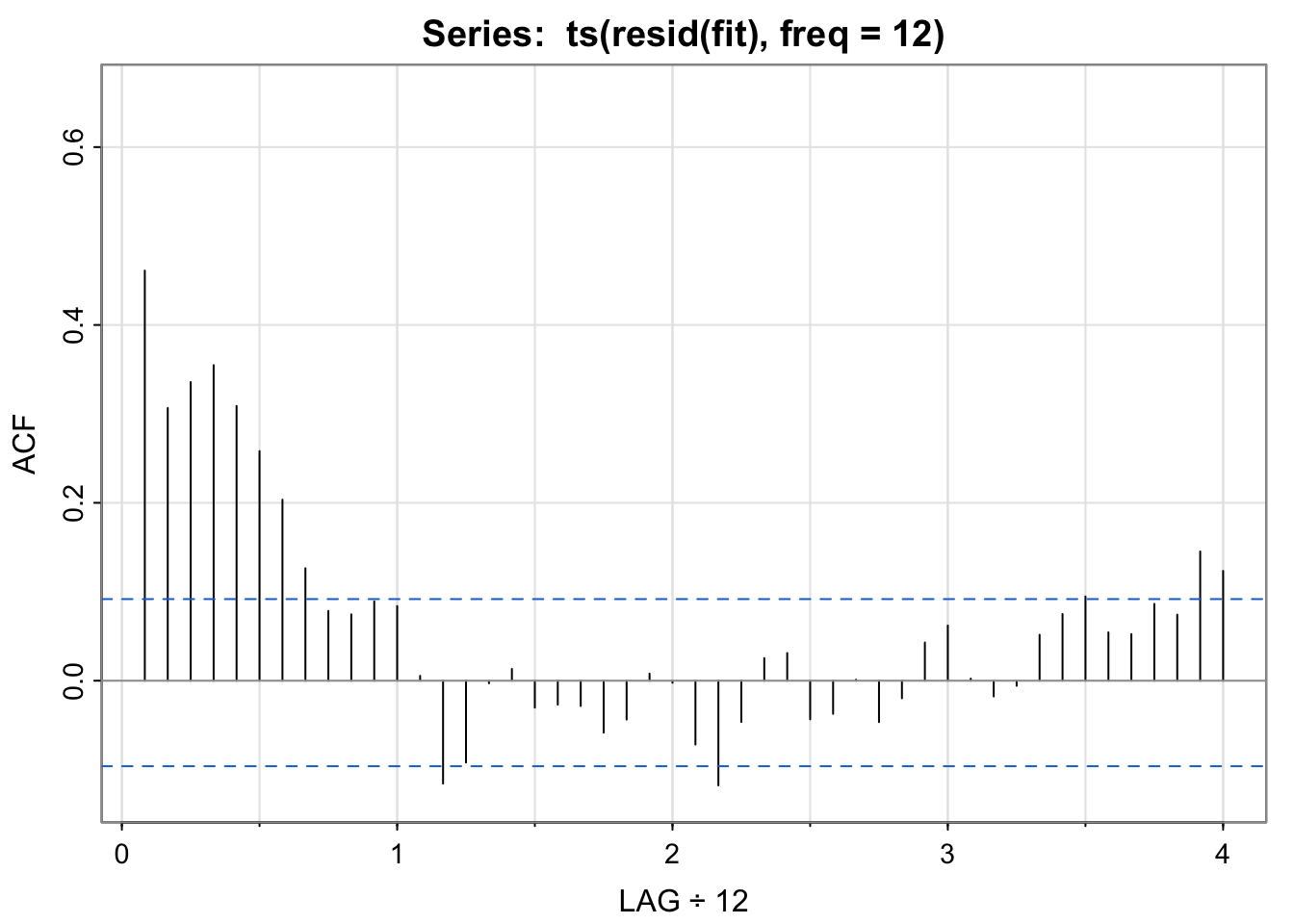

##  [1]  0.46  0.31  0.34  0.35  0.31  0.26  0.20  0.13  0.08  0.07  0.09  0.08
## [13]  0.01 -0.12 -0.09  0.00  0.01 -0.03 -0.03 -0.03 -0.06 -0.04  0.01  0.00
## [25] -0.07 -0.12 -0.05  0.03  0.03 -0.04 -0.04  0.00 -0.05 -0.02  0.04  0.06
## [37]  0.00 -0.02 -0.01  0.05  0.07  0.09  0.05  0.05  0.09  0.07  0.15  0.12
  1. What’s the difference between the model estimated in fit above vs. in Activity 2?

Here, we are modeling the real soi data, not the simulated data. However, we are using the same format of the model (just estimating the two amplitudes, one each for the sine and cosine terms).

  1. What is the equation of the estimated seasonal trend?

\[ \hat{x} = 0.313\cos \left (\frac{2\pi t}{12} \right) +0.073 \sin \left (\frac{2\pi t}{12} \right ) \]

  1. Does the temporal structure in soi appear to be captured by the seasonal model?

No. If the temporal structure were captured, the acf of the residuals would look like white noise, but it does not. (Harmonics??)

  1. Why convert to a time series before plotting the sample acf?

This is to make the lag comparable to the other acf plots we were looking at earlier. The residual series resid(fit) is just a vector, not a ts, so the acf will assume a frequency of 1, or monthly. The shape of the plot will look the same, it’s just a labeling consistency thing that captures the annual pattern.

Choosing the seasonal index

  • If you have quarterly data, period is 4 (freq 1/4)
  • If you have monthly data, period is 12 (freq 1/12)
  • If you have weekly data, period is 52 (freq 1/52)
  • If you have daily data, period is 365.25 (freq 1/365.25)

There might be cases where the frequency is something else, but maybe not in the context of annual seasonality.

Activity 4

What is the period for the following seasonal patterns for data collected every minute?

  • Hourly

  • Daily

  • Weekly

  • Monthly

Activity 4 Solutions

What is the period for the following seasonal patterns for data collected every minute?

  • Hourly: 60

  • Daily: 60*24 = 1440

  • Weekly: 1440*7 = 10080

  • Monthly = 60*24*30 = 43,200 (approximation)

  • Yearly = 60*24*365.25 = 525,960

More complicated “seasonality”

Code 
#install.packages("lubridate")
library(lubridate)
?period

A note on terminology

Concept Term in S&S (red book) Term in FPP (free book)
Variation between a max and a min (fixed period) cyclic (introduced as precise seasonality after talking about seasonal differencing in SARIMA model section) seasonal
Variation between a max and a min (random period) pseudo*-cyclic cyclic

*pseudo means “false”

The same word can mean very different things. Yikes!!! This is why we need a little math (understanding what a period is) to be able to communicate successfully about time series.

Example 3.13/3.14

I skipped over the lagplots of