Code
## Simulate random walk w/ drift
## your code here Lecture 5
Link to Slides w/ Solutions
Link to template
\[ \newcommand\E{{\mathbb{E}}} \]
Last time
- Trend Stationarity model
- Salmon price example
- Simulating a time series to understand the autocovariance function
Today
- Time series at ENVR Conference
- Detrending
- Activities
- Differencing
A look ahead
- Weeks 1-2: terminology of time series models, working with various R functions relating to time series (Chapters 1-2)
- Week 3: Trends, trends, trends (smoothing) (Chapters 2-3 in Shumway and Stoffer, Ch 8 in FPP)
- Week 4: Time series regression (trends that depend on predictor variables), Forecasting (Chapter 5 and 7 in FPP)
- Week 5: Time series data science process, and midterm (Chapter 5 in FPP, various parts in Shumway and Stoffer)
- Week 6: Partial correlation and ARMA models (Chapter 4 in Shumway and Stoffer)
- Week 7: ARIMA models (what they are, when to use them, and how to know if yours is trash) (Chapter 4 in Shumway and Stoffer, Chapter 9 in FPP)
- Week 8: Cross-correlation and Multiple time series (Ch 2, Ch 3 in Shumway and Stoffer)
- Week 9: Wiggle room/class choice
- Week 10: Wiggle room/class choice
Time series at the ENVR Conference
Is a “trend” necessarily linear?
- Oh no, I have to talk to the intimidating experts
- The very first talk: “A trend doesn’t have to be linear”- Robert Lund
- The penultimate talk: “seasonal trend”
Conclusion:
- Nope! Seems like “trend” = “mean function”
Lots of examples of vocab we’ve learned…
Notes on Robert Lund’s Talk
Notes on Robert Lund’s Talk
Notes from Matthias Katzfuss’s talk
Notes from Dan Cooley’s talk
Notes from Dan Cooley’s talk
Detrending
Detrending
If a process is trend stationary (nonstationary in the mean, but stationary in the variance), can we just subtract off the trend and get back a stationary time series?
Sometimes (assuming we are able to estimate it), and that’s called detrending.
Goal:
Assuming trend stationarity (\(x_t = \mu_t + y_t\), where \(y_t\) is stationary), find an estimate \(\widehat{\mu}_t\) and compute
\[ \begin{align} \widehat{y_t} &= x_t - \widehat{\mu_t}\\ \text{Estimated Stationary process} &= \text{Data - trend estimate} \end{align} \] Note: Does \(y_t\) remind you of anything from regression?
Example: Subtracting off the trend
- Dark yellow line: the trend estimate
- black: The observed data
- shaded region: 95% confidence bands on trend estimates.
Can we make the time series stationary by subtracting off the trend?
Example: Subtracting off the trend
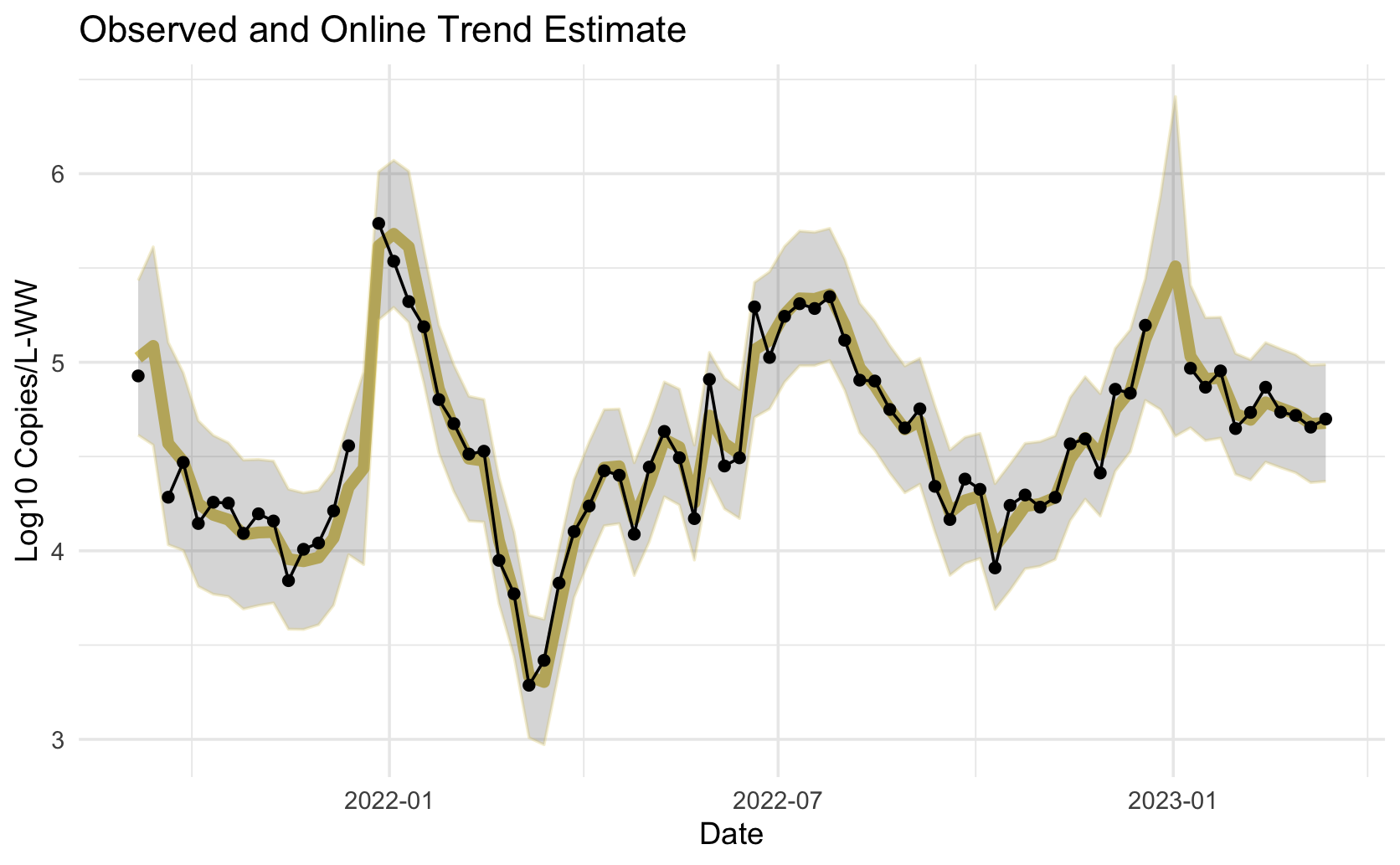
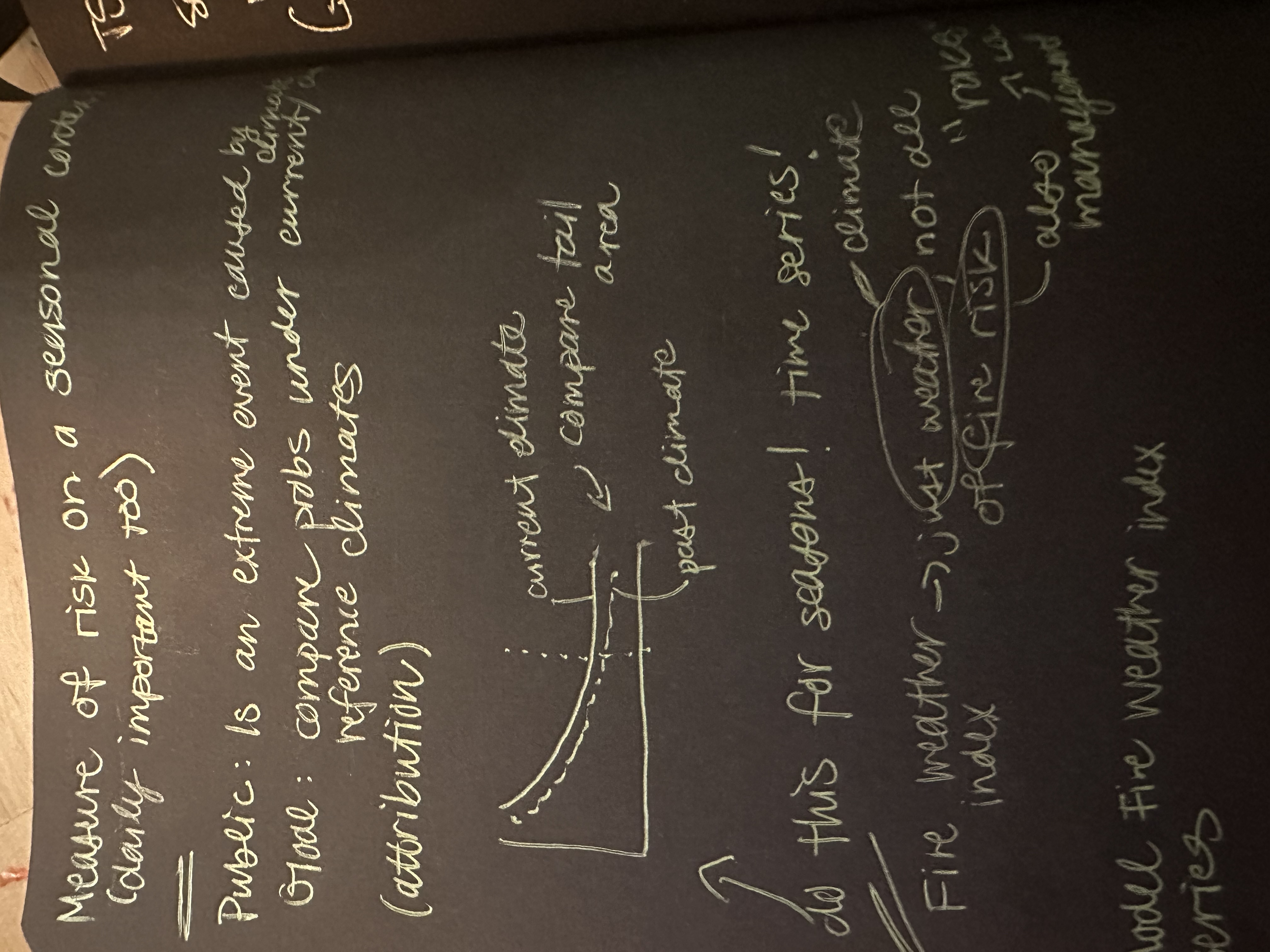
Does this time series appear stationary? In the mean, yes.
Example: Subtracting off the trend
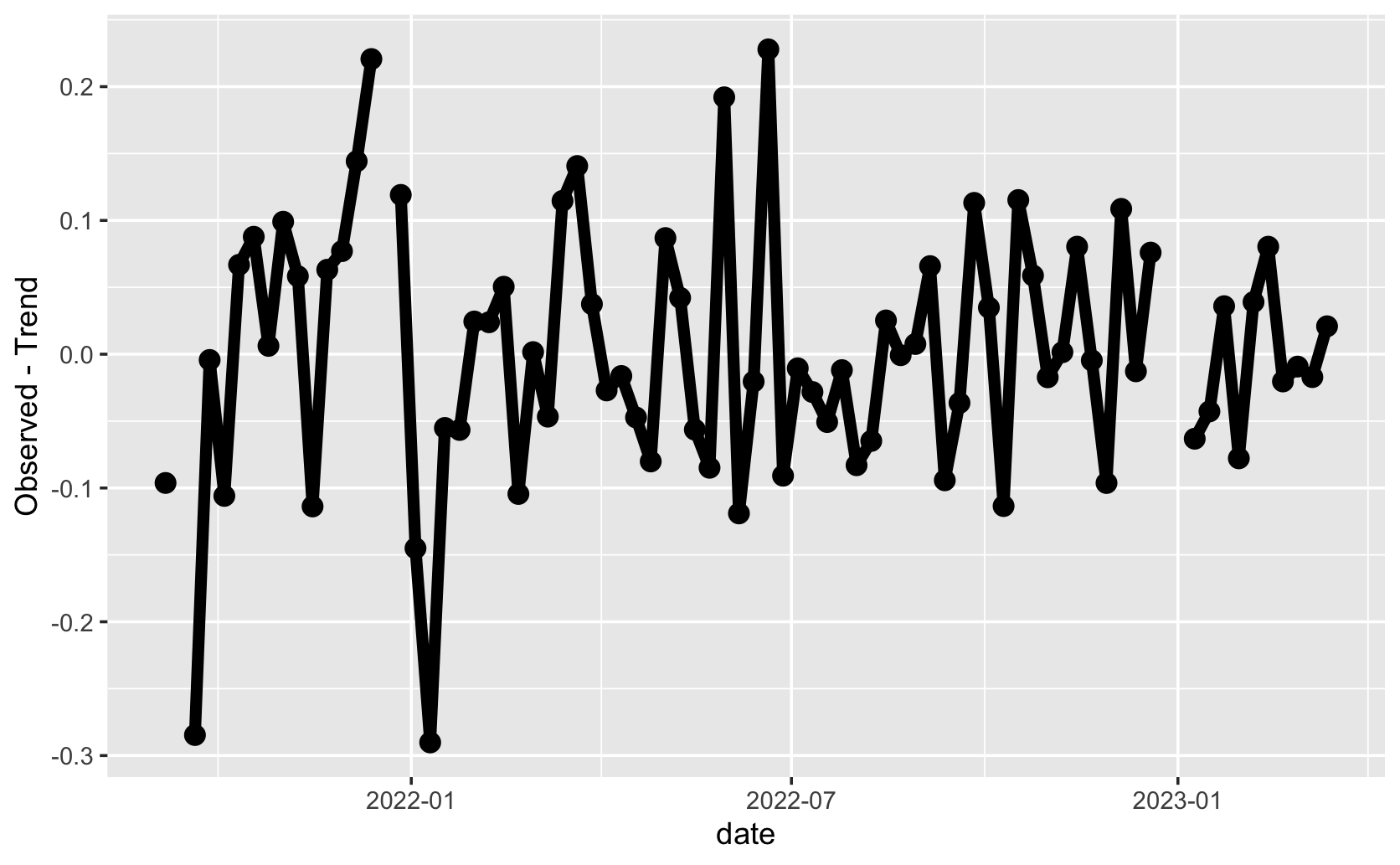
Have we captured the temporal structure in the time series? Yes (note: we will learn about ACF hypothesis tests/p-values during the “time series data analysis process”)
Aside: managing a time series project code base
- I manage the GitHub for Houston Wastewater Epidemiology
- Check out the “issues”
- Section 1: Demo adding new issue (“basic” time series methods)
- Section 2: Demo adding new issue (link to definition of online estimation)
Activity 1: Detrending a commodity (Example 3.7)
- Given the code to generate the plot with the trend line, how would you view the equation of the trend line?
- Visualize the de-trended series. Does it appear stationary?
- Compute the acf of the salmon series and the detrended series. What do you notice?
Activity 1 Solutions
Use Lecture5Template.qmd
Activity 2: “assuming we are able to estimate it”
- Look at pages 37-41 of the textbook
- what is “it” in this context? (what are we estimating?)
- If this is review, where did you first see these ideas?
- Put a dot on the math anxiety rating distribution on the back board
Activity 2Solutions: “assuming we are able to estimate it”
Use Lecture5Template.qmd
Differencing
Motivation/model
Consider the trend stationary model (\(y_t\) is stationary). \[ x_t = \mu_t + y_t \] We saw how to estimate a fixed trend using a linear regression for the mean (\(\mu_t = \beta_0 + \beta_1t\))
We then subtract off the estimate of the trend (detrend), \(\widehat{\mu_t}\) so that we are working with a stationary time series:
\[ \widehat{y_t} = x_t - \widehat{\mu_t} \]
What if the trend was not fixed? (dependent on \(t\) beyond just “\(t\) as a constant”)
A stochastic trend model
Change the model for the mean to incorporate a stochastic component (random walk with drift):
\[ \mu_t = \delta + \mu_{t-1} + w_t \] Where \(w_t\) is white noise independent of \(y_t\).
Is \(\mu_t\) stationary? No (it’s a random walk, nonstationary in both mean and covariance)
How to “get back” to a stationary time series?
Since the stochastic component depends on just one past time point, consider the series \(x_t - x_{t-1}\).
This series is called the differenced series and the process is called differencing.
Computing the difference series in terms of the (stochastic) trend model
\[ \begin{align} x_{t} - x_{t-1} &= (\mu_t + y_t) - (\mu_{t-1} - y_{t-1})\\ &= (\delta + \mu_{t-1} + w_t + y_t) - (\mu_{t-1} - y_{t-1})\\ & = \delta + w_t + y_t - y_{t-1} \end{align} \] Need to compute mean function \(\E(x_t - x_{t-1}\) and autocovariance function \(cov(x_t - x_{t-1}, x_s- x_{s-1})\) and check if they do not depend on \(t\) (mean) and just depend on the lag \(h = s-t\).
…But the answer is we do get a stationary series!
Activity 3: Simulating a random walk and then differencing it
- Simulate a random walk with no drift and plot it.
- Use the
difffunction to difference the simulated series. Plot the result.
Code
# your code here- Does this series appear stationary? How do you know?
- Visualize the ACF of the differenced series. Does it look like white noise?
Code
# your code hereActivity 4: Differencing Salmon Prices
- Compute and plot the differenced salmon series.
Code
# your code here- Does the series appear stationary?
- Visualize the acf of the differenced series. Does it look like white noise?
Activity 5: Comparing Differencing and Detrending
Compare the Acfs of the differenced and detrended salmon series. What do you notice?
Code
# your code hereNext time: Smoothing
We’ve seen three explicity ways of modeling a trend (moving average (hw 1), and regression with time and random walk).
How else could we model a trend?
Visual example:
Code
tsplot(soi, col=4)
lines(ksmooth(time(soi), soi, "normal", bandwidth=1), lwd=2, col=6)
par(fig = c(.65, 1, .75, 1), new = TRUE) # the insert
curve(dnorm, -3, 3, xaxt='n', yaxt='n', ann=FALSE)