Lecture 6

Recap

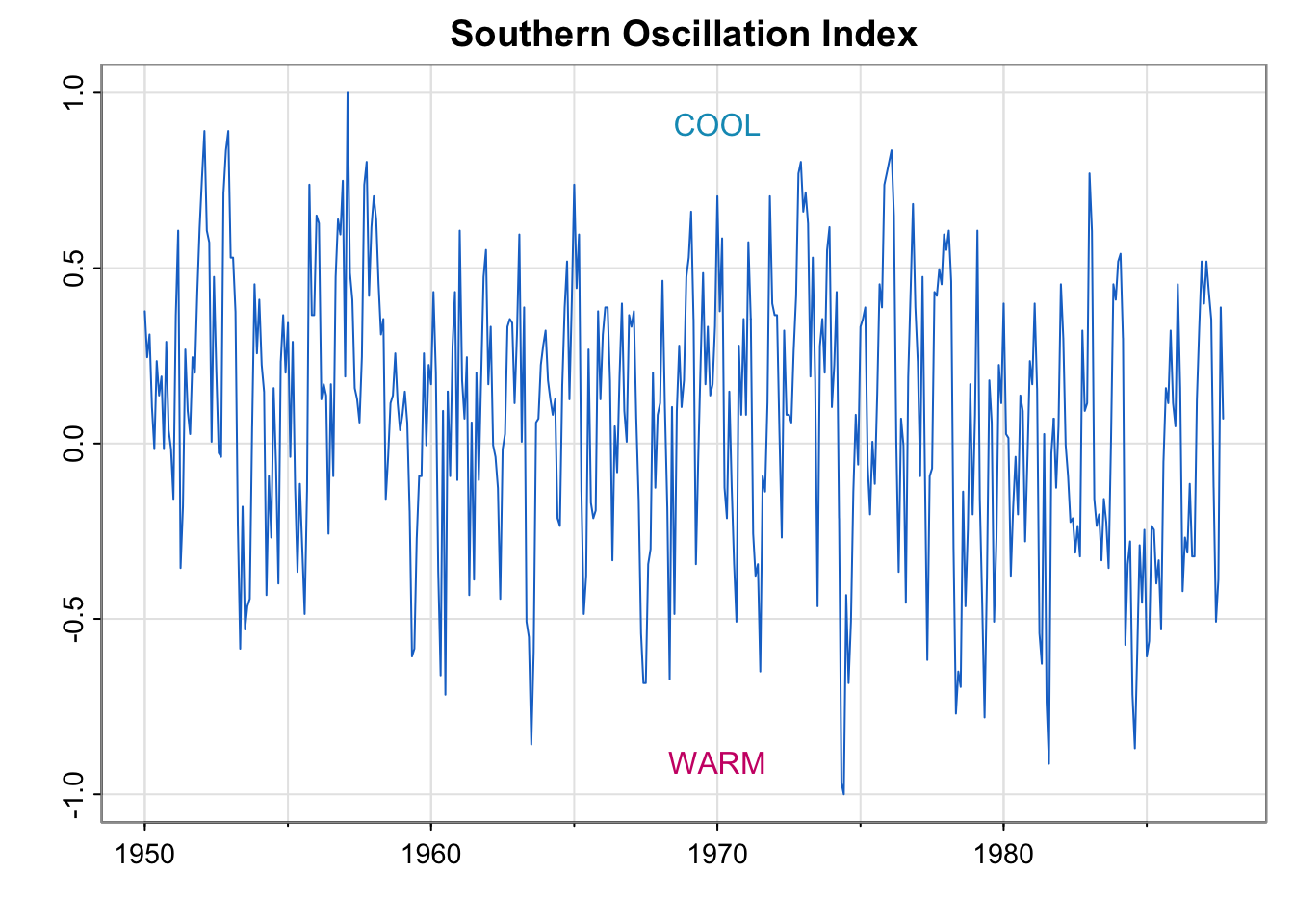
\[ \newcommand\E{{\mathbb{E}}} \]

We’ve been estimating trends and getting confused about stationarity :)

A look ahead

Next few weeks:

• Assignment 3 posted soon, Due Friday, October 18, we will review in class on Monday prior to midterm
• Next Monday: remote class: activity to start your “cheat sheet” and a data analysis challenge
• Sometime next week: Practice midterm posted

Where is the template file?

• We are going to create it, and you will submit a rendered pdf of today’s lecture as your “participation”.

Getting organized with Quarto

Create a folder somewhere on your computer called “Lecture6”.

Open R studio, and create a .qmd File and save inside the “Lecture6” folder as “Yourname_Lecture6.qmd”.

Create a header for Activity 1.

Today

• Review: Stationarity, White Noise, Autocovariance, and “temporal structure”
• Smoothing

Activity 1: In groups:

Choose two properties from:

• Stationarity
• White Noise
• Autocovariance, and
• “temporal structure”

Define the properties in symbols and words and describe why they are different. Make sure to put this in your quarto file!

When you’re done, share with another group. Put that group’s answer under another header.

Go around and share as a class.

• Add one or two observations from other groups

Data set focus: SOI

Code Source

More about SOI on Climate.gov

library(astsa)
tsplot(soi, ylab="", xlab="", main="Southern Oscillation Index", col=4)
text(1970, .91, "COOL", col=5)
text(1970,-.91, "WARM", col=6)

Activity 2: Moving average smoother (Example 3.16)

Code source

library(astsa)
#library(tidyverse)
## 
w = c(.5, rep(1,11), .5)/12
soif = filter(soi, sides=2, filter=w)
tsplot(soi, col=astsa.col(4,.7), ylim=c(-1, 1.15))
lines(soif, lwd=2, col=4)
# insert
par(fig = c(.65, 1, .75, 1), new = TRUE)
w1 = c(rep(0,20), w, rep(0,20))
plot(w1, type="l", ylim = c(-.02,.1), xaxt="n", yaxt="n", ann=FALSE)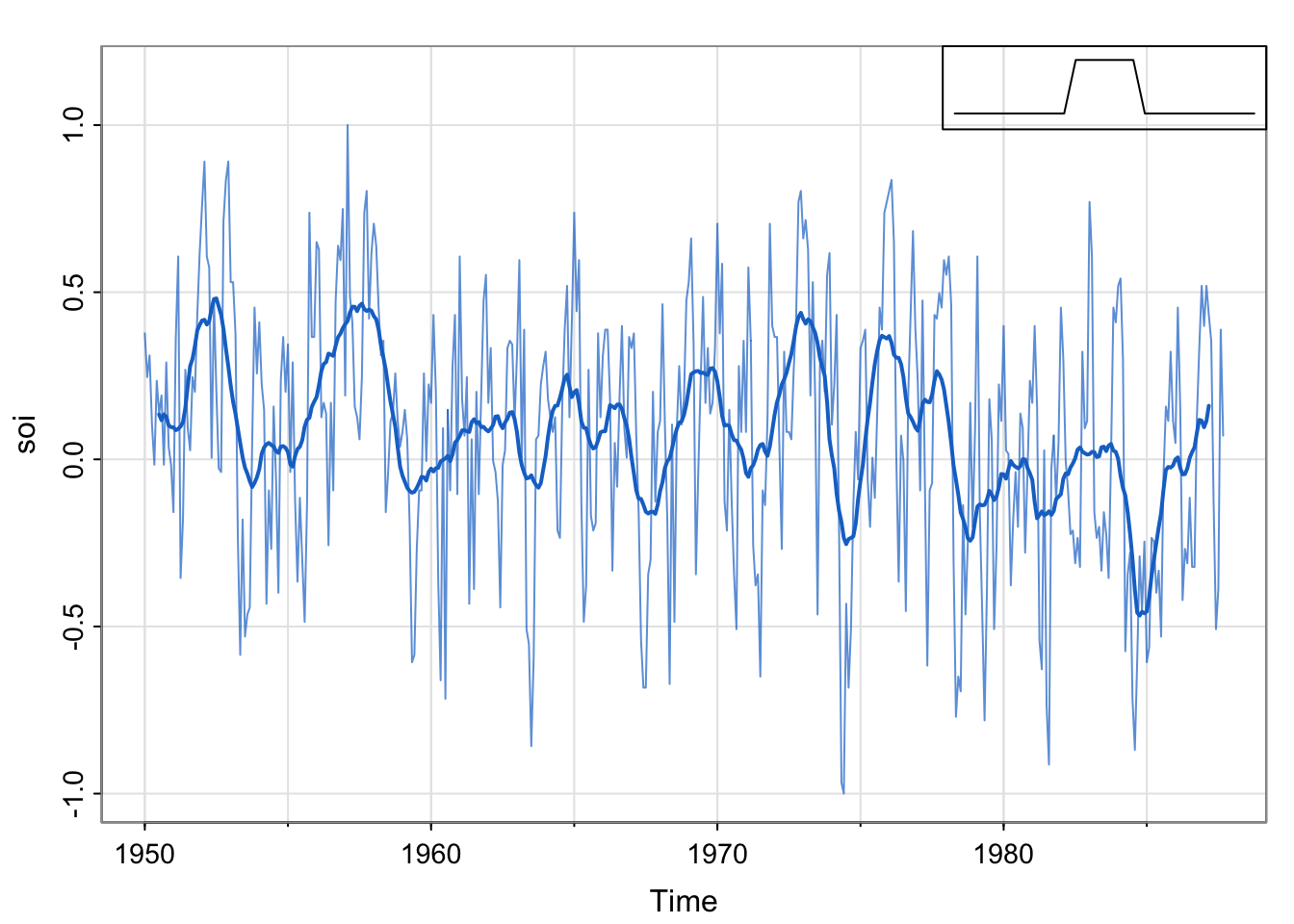

par(mfrow = c(1,1))

## Detrend

## Plot detrended

## acfs

0. The code gives an error. Can you fix it?
1. Does the moving average smoother appear to be doing a good job of capturing the trend?
2. Detrend the soi series with respect to the moving average smoother.
3. Plot the detrended soi series
4. Compute the acf of the soi series and detrended series. What do you notice?

Activity 2 Solution

library(astsa)
library(tidyverse)

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.3     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

## 
w = c(.5, rep(1,11), .5)/12
soif = stats::filter(soi, sides=2, filter=w)
tsplot(soi, col=astsa.col(4,.7), ylim=c(-1, 1.15))
lines(soif, lwd=2, col=4)
par(fig = c(.65, 1, .75, 1), new = TRUE)
w1 = c(rep(0,20), w, rep(0,20))
plot(w1, type="l", ylim = c(-.02,.1), xaxt="n", yaxt="n", ann=FALSE)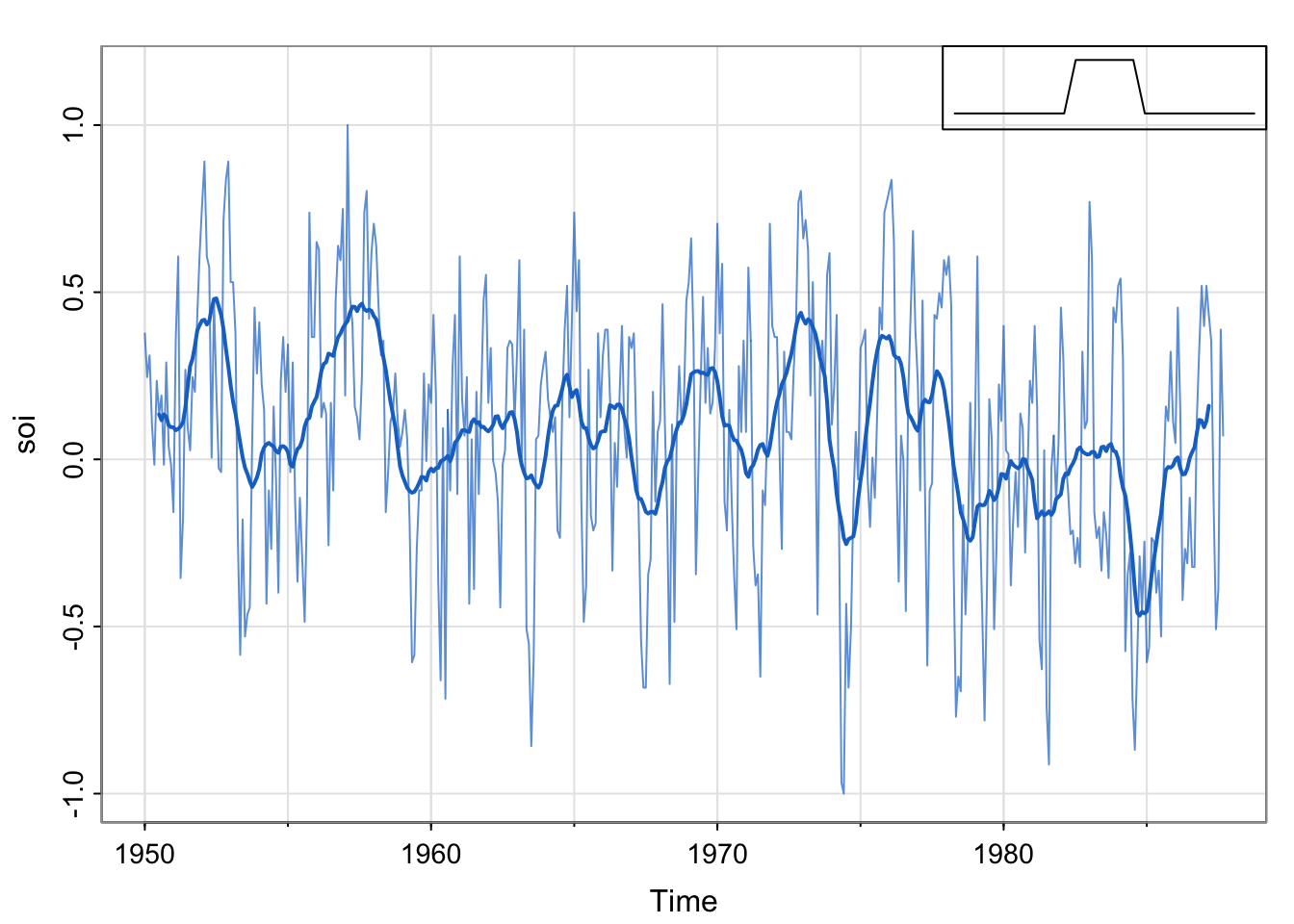

par(mfrow = c(1,1))

## Detrend
detrended <- soi-soif

## Plot detrended
tsplot(detrended)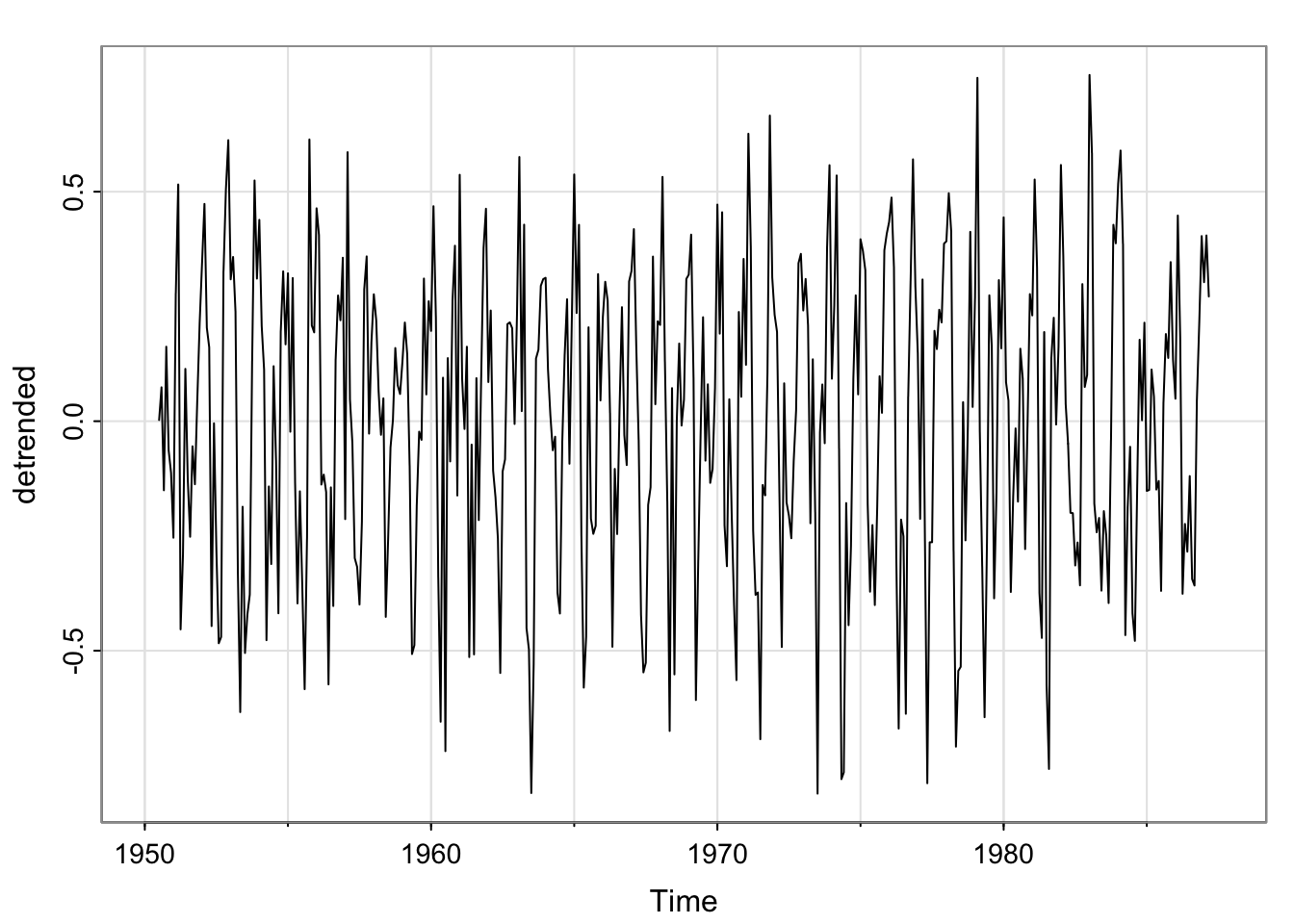

## acfs
acf1(soif, na.action = na.pass)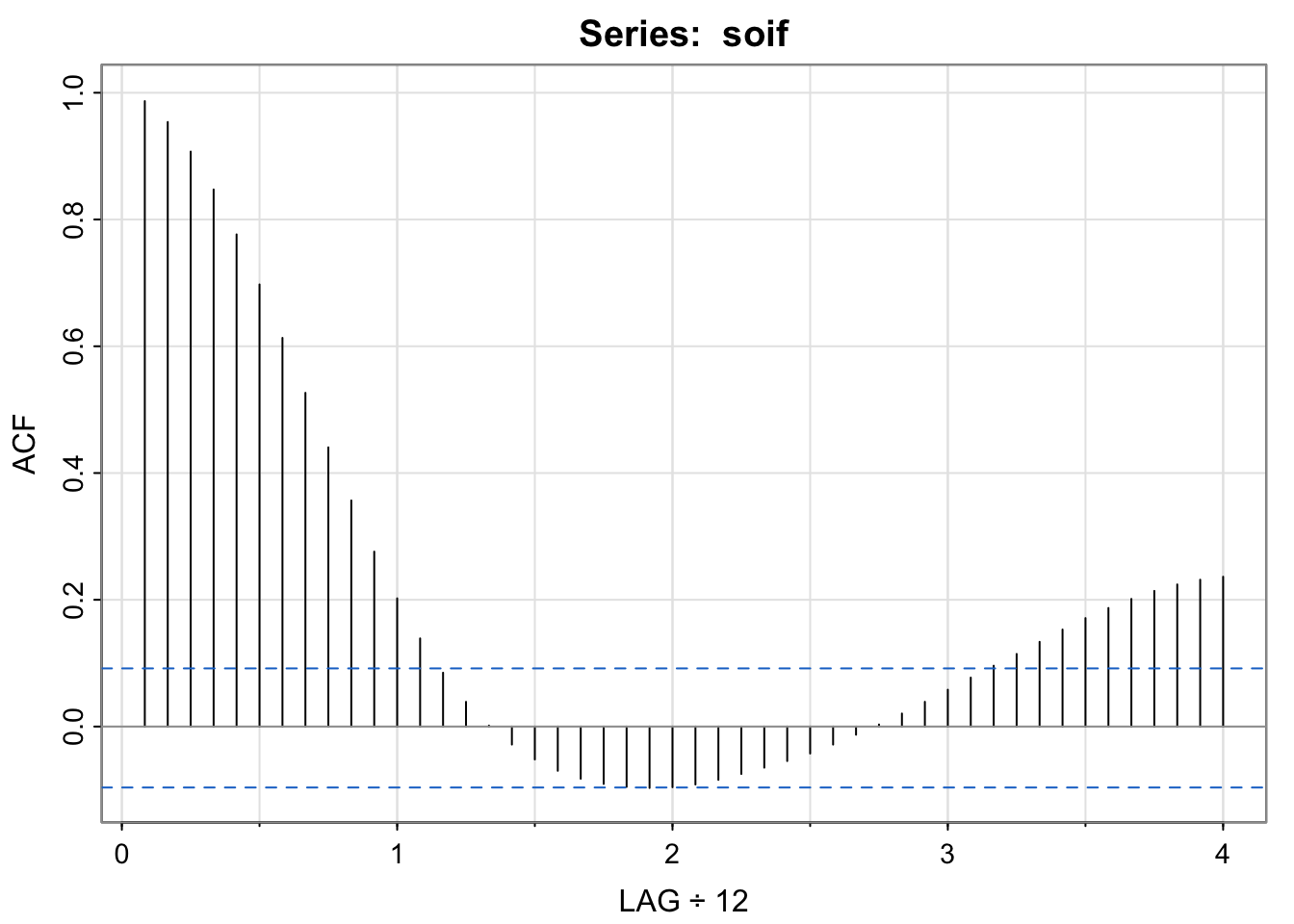

 [1]  0.99  0.95  0.91  0.85  0.78  0.70  0.61  0.53  0.44  0.36  0.28  0.20
[13]  0.14  0.08  0.04  0.00 -0.03 -0.05 -0.07 -0.08 -0.09 -0.10 -0.10 -0.10
[25] -0.09 -0.08 -0.07 -0.06 -0.05 -0.04 -0.03 -0.01  0.00  0.02  0.04  0.06
[37]  0.08  0.10  0.11  0.13  0.15  0.17  0.19  0.20  0.21  0.22  0.23  0.24

par(mfrow = c(2,1))
acf1(soi)

 [1]  0.60  0.37  0.21  0.05 -0.11 -0.19 -0.18 -0.10  0.05  0.22  0.36  0.41
[13]  0.31  0.10 -0.06 -0.17 -0.29 -0.37 -0.32 -0.19 -0.04  0.15  0.31  0.35
[25]  0.25  0.10 -0.03 -0.16 -0.28 -0.37 -0.32 -0.16 -0.02  0.17  0.33  0.39
[37]  0.30  0.16  0.00 -0.13 -0.24 -0.27 -0.25 -0.13  0.06  0.21  0.38  0.40

acf1(detrended, na.action = na.pass)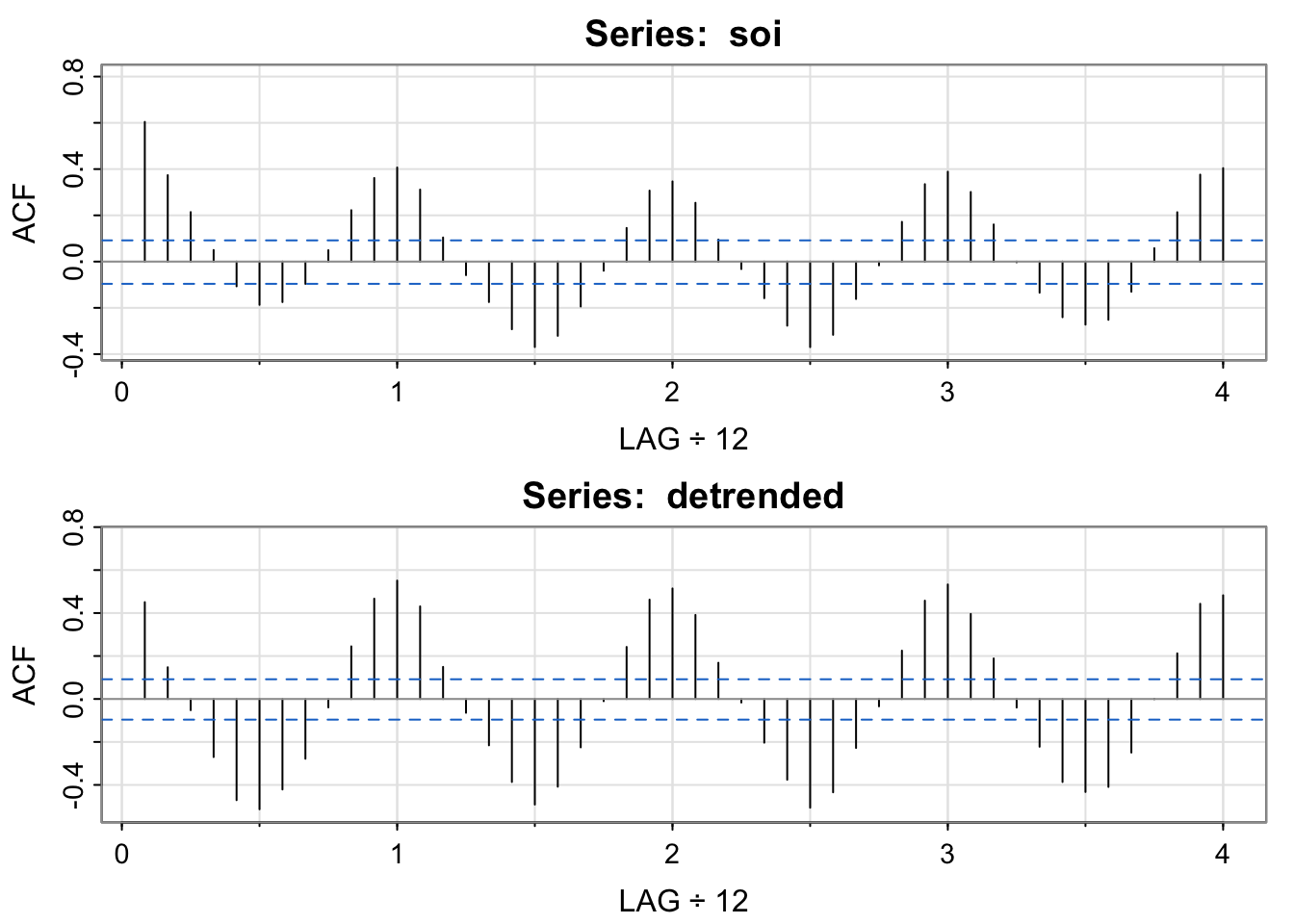

 [1]  0.45  0.15 -0.05 -0.27 -0.47 -0.51 -0.42 -0.28 -0.04  0.24  0.47  0.55
[13]  0.43  0.15 -0.06 -0.22 -0.39 -0.49 -0.41 -0.23 -0.01  0.24  0.46  0.51
[25]  0.39  0.17 -0.02 -0.20 -0.38 -0.51 -0.43 -0.23 -0.03  0.22  0.46  0.53
[37]  0.40  0.19 -0.04 -0.22 -0.39 -0.43 -0.41 -0.25  0.00  0.21  0.44  0.48

0. The code gives an error. Can you fix it? We need to specify we want stats::filter not dplyr::filter
1. Describe the trend estimated by the moving average smoother. The moving average smoother smooths out the annual cycles (the shorter oscillations in the observed series) and emphasizes a longer range cycle– this is the El Niño pattern.
2. Detrend the soi series with respect to the moving average smoother. Here, we just subtract the estimated trend from the observed series. Note that there will be missing values on the ends, but that’s ok.
3. Plot the detrended soi series
4. Plot the acf of the soi series, the moving average trend estimate, and detrended series. What do you notice?

The soi and detrended soi have similar acfs that both appear to reveal the annual cycle, though the magnitude of the correlations are different. The moving average smoother shows the longer term oscillation. Each of these series has temporal structure (does not look like white noise).

What is a moving average smoother?

\[ m_t = \sum_{j = -k}^k a_j x_{t-j} \]

Where \(x_t\) is any time series and the coefficients add to 1. How is this different from the “moving average model”?

• In the model we’ve seen so far, we assume \(x_t\) is white noise and that the weights are equal

What were the weights in the last example? How do you know? soif = stats::filter(soi, sides=2, filter=w) is portion of the code that computes the moving average. The weights are in the filter argument, so we need to look at what w is:

w

 [1] 0.04166667 0.08333333 0.08333333 0.08333333 0.08333333 0.08333333
 [7] 0.08333333 0.08333333 0.08333333 0.08333333 0.08333333 0.08333333
[13] 0.04166667

plot(-6:6, w, ylim = c(0, .1), ylab = "Weight", xlab = "distance from point we want the moving average estimate for")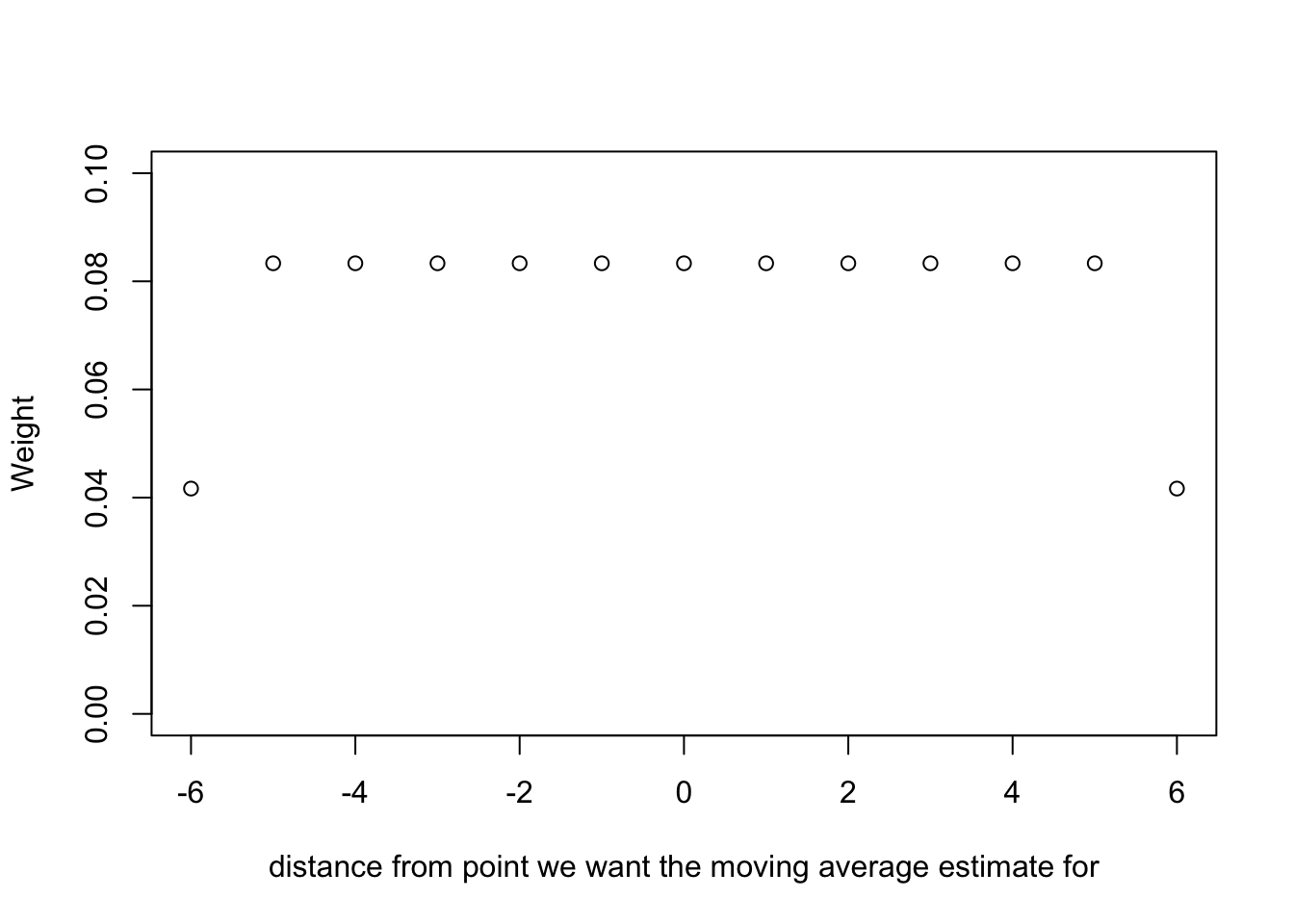

Activity 3: Kernel smoothing (Example 3.17)

Code source

tsplot(soi, col=4)
lines(ksmooth(time(soi), soi, "normal", bandwidth=1), lwd=2, col=6)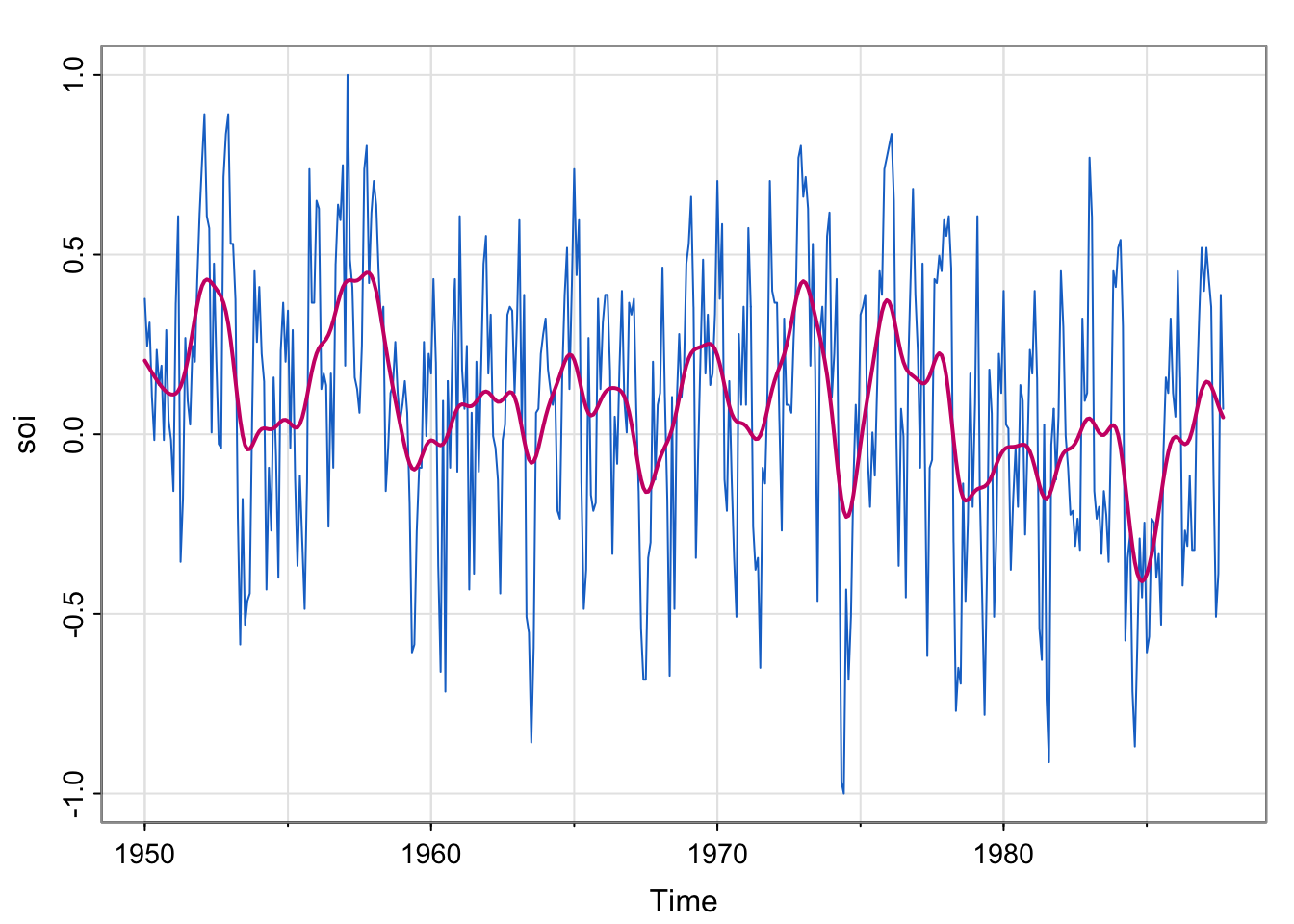

## detrend

## plot detrended

## acfs

1. Describe the trend captured by the kernel smoother.
2. Change the bandwith to 2 and re-plot the kernel smoother and soi series. Repeat with a bandwidth of 0.5. What do you think the bandwidth parameter does?
3. Detrend the soi series with respect to the kernel smoother.
4. Plot the detrended soi series
5. Plot the acf of the soi series, the kernel trend estimate, and detrended series. What do you notice?

Activity 3 Solution

Code source

tsplot(soi, col=4, ylim = c(-1, 1.15))
lines(ksmooth(time(soi), soi, "normal", bandwidth=1), lwd=2, col=6)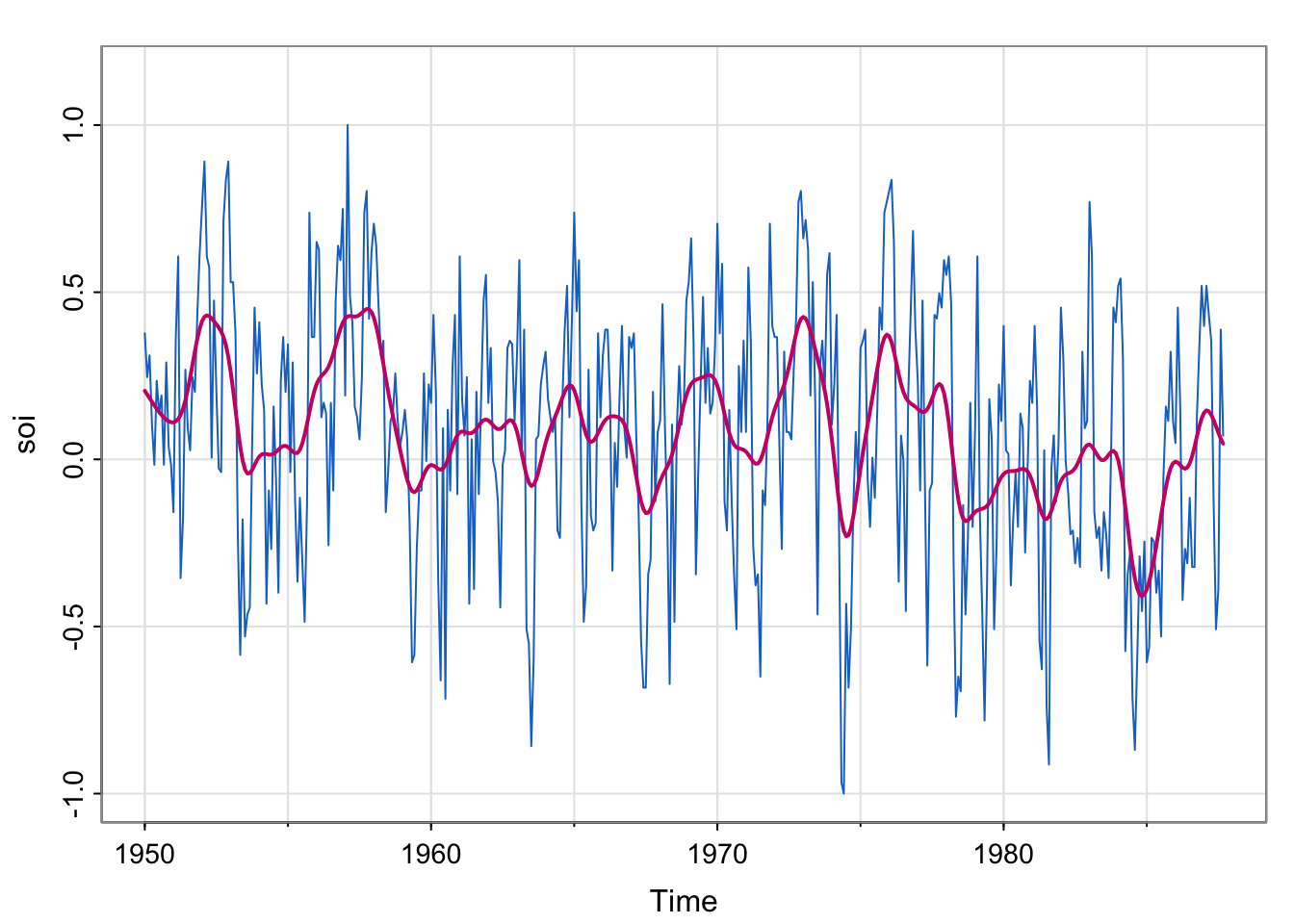

## change bandwidth
tsplot(soi, col=4, ylim = c(-1, 1.15))
lines(ksmooth(time(soi), soi, "normal", bandwidth=2), lwd=2, col=6)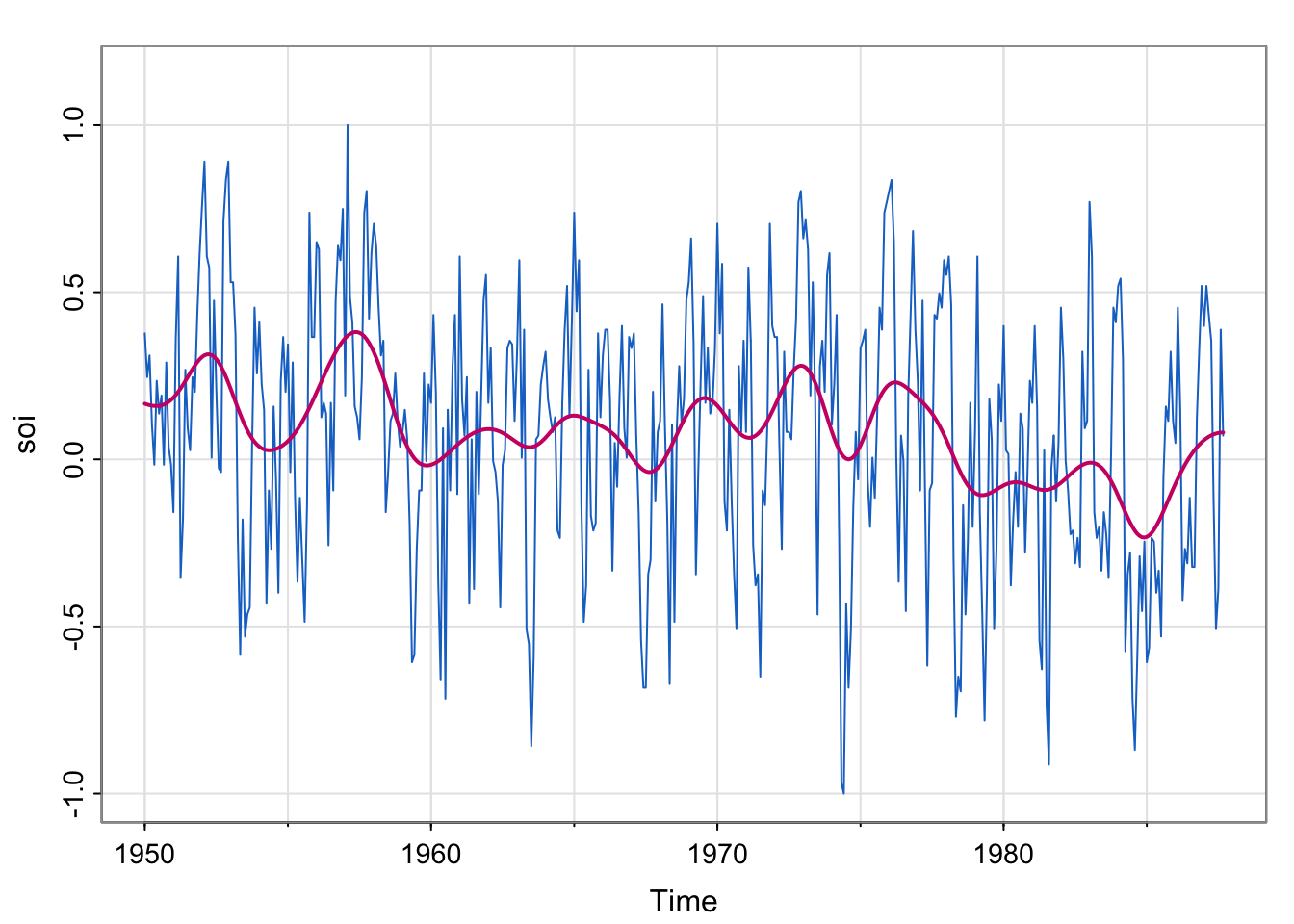

tsplot(soi, col=4, ylim = c(-1, 1.15))
lines(ksmooth(time(soi), soi, "normal", bandwidth=0.5), lwd=2, col=6)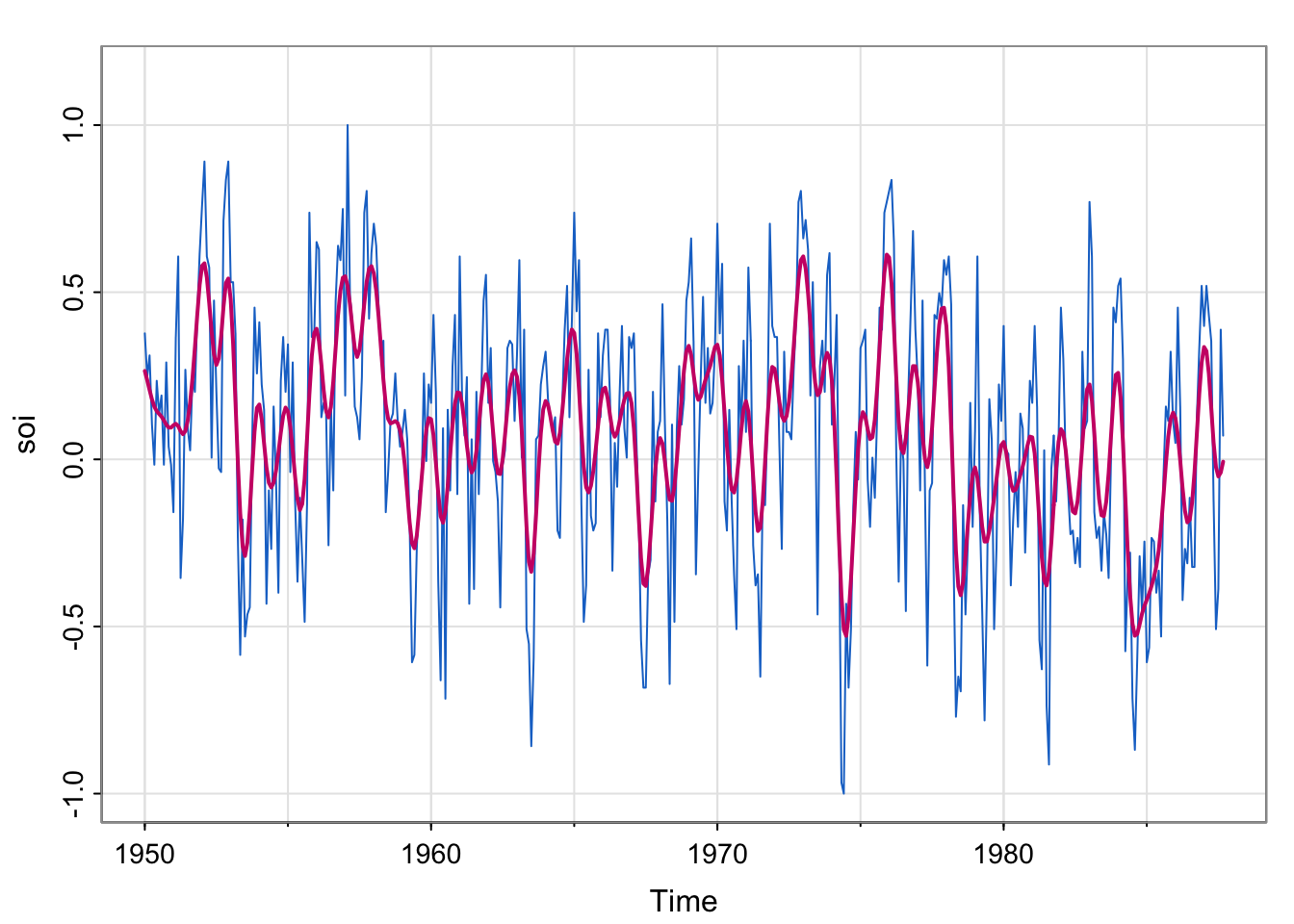

## Detrend
soi_ksmooth <- ksmooth(time(soi), soi, "normal", bandwidth=1)
detrended <- soi-soi_ksmooth$y

## Plot detrended
tsplot(detrended)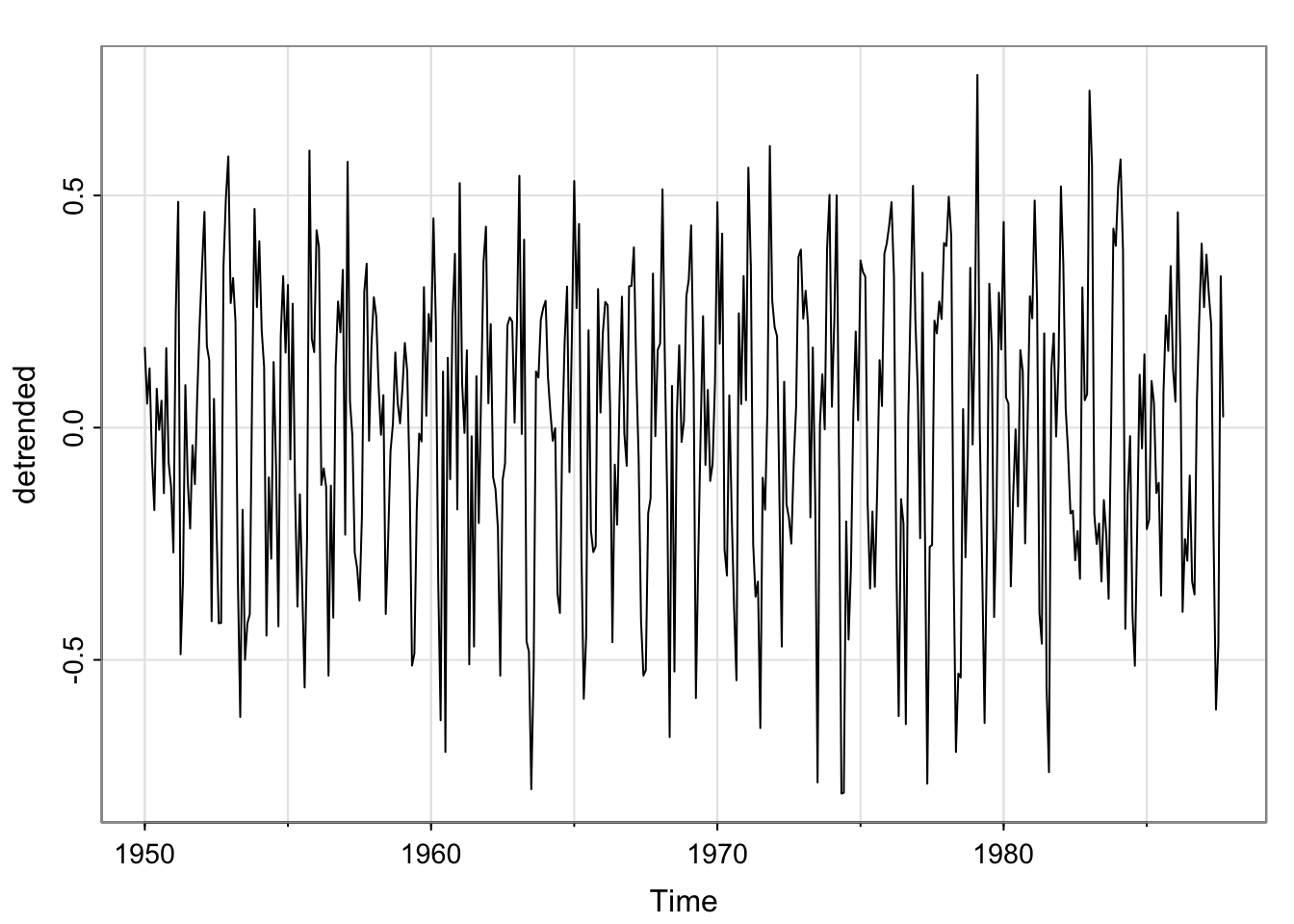

## acfs
acf1(soi_ksmooth$y, na.action = na.pass)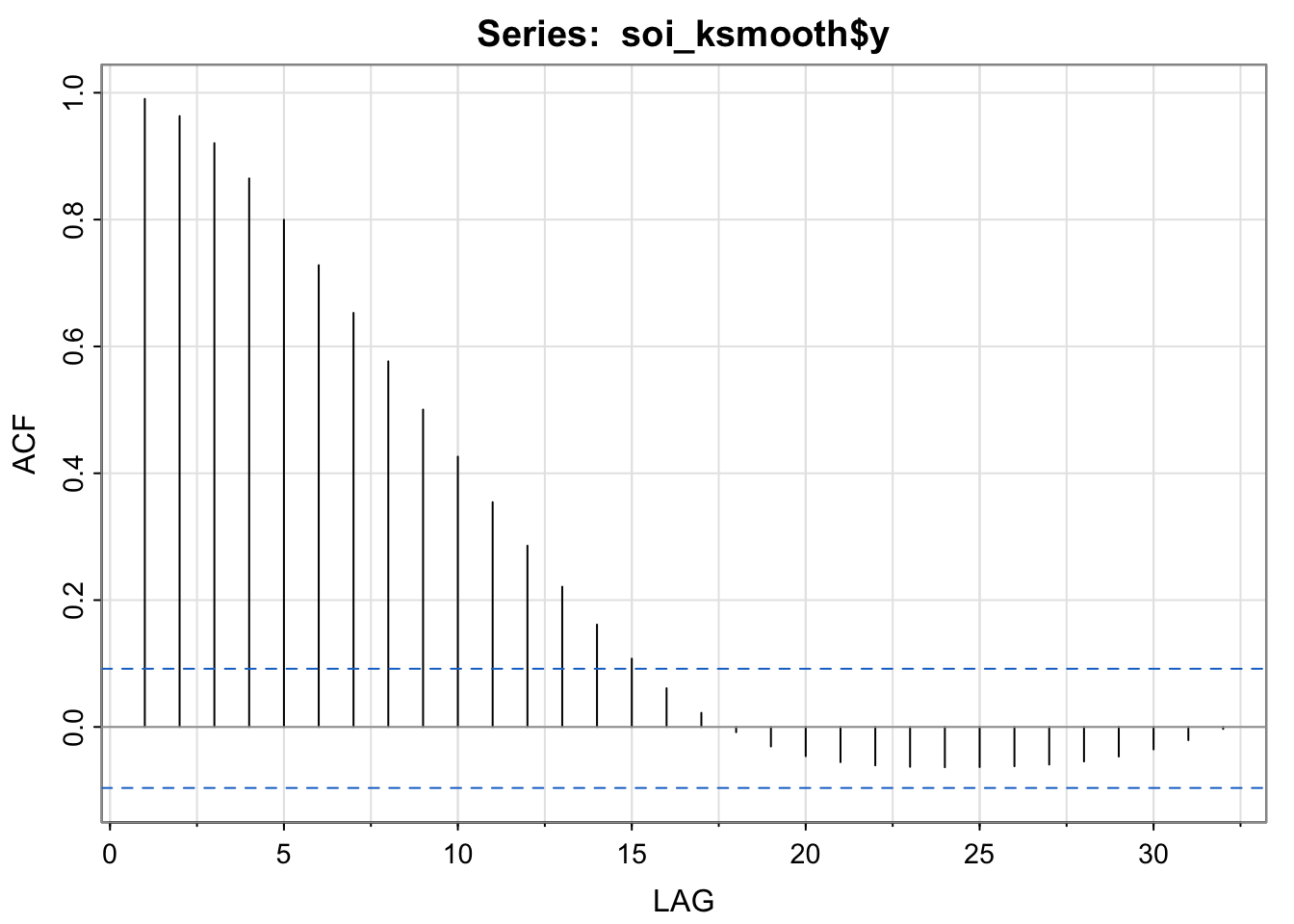

 [1]  0.99  0.96  0.92  0.86  0.80  0.73  0.65  0.58  0.50  0.43  0.35  0.29
[13]  0.22  0.16  0.11  0.06  0.02 -0.01 -0.03 -0.05 -0.06 -0.06 -0.06 -0.06
[25] -0.06 -0.06 -0.06 -0.05 -0.05 -0.04 -0.02  0.00

par(mfrow = c(2,1))
acf1(soi)

 [1]  0.60  0.37  0.21  0.05 -0.11 -0.19 -0.18 -0.10  0.05  0.22  0.36  0.41
[13]  0.31  0.10 -0.06 -0.17 -0.29 -0.37 -0.32 -0.19 -0.04  0.15  0.31  0.35
[25]  0.25  0.10 -0.03 -0.16 -0.28 -0.37 -0.32 -0.16 -0.02  0.17  0.33  0.39
[37]  0.30  0.16  0.00 -0.13 -0.24 -0.27 -0.25 -0.13  0.06  0.21  0.38  0.40

acf1(detrended, na.action = na.pass)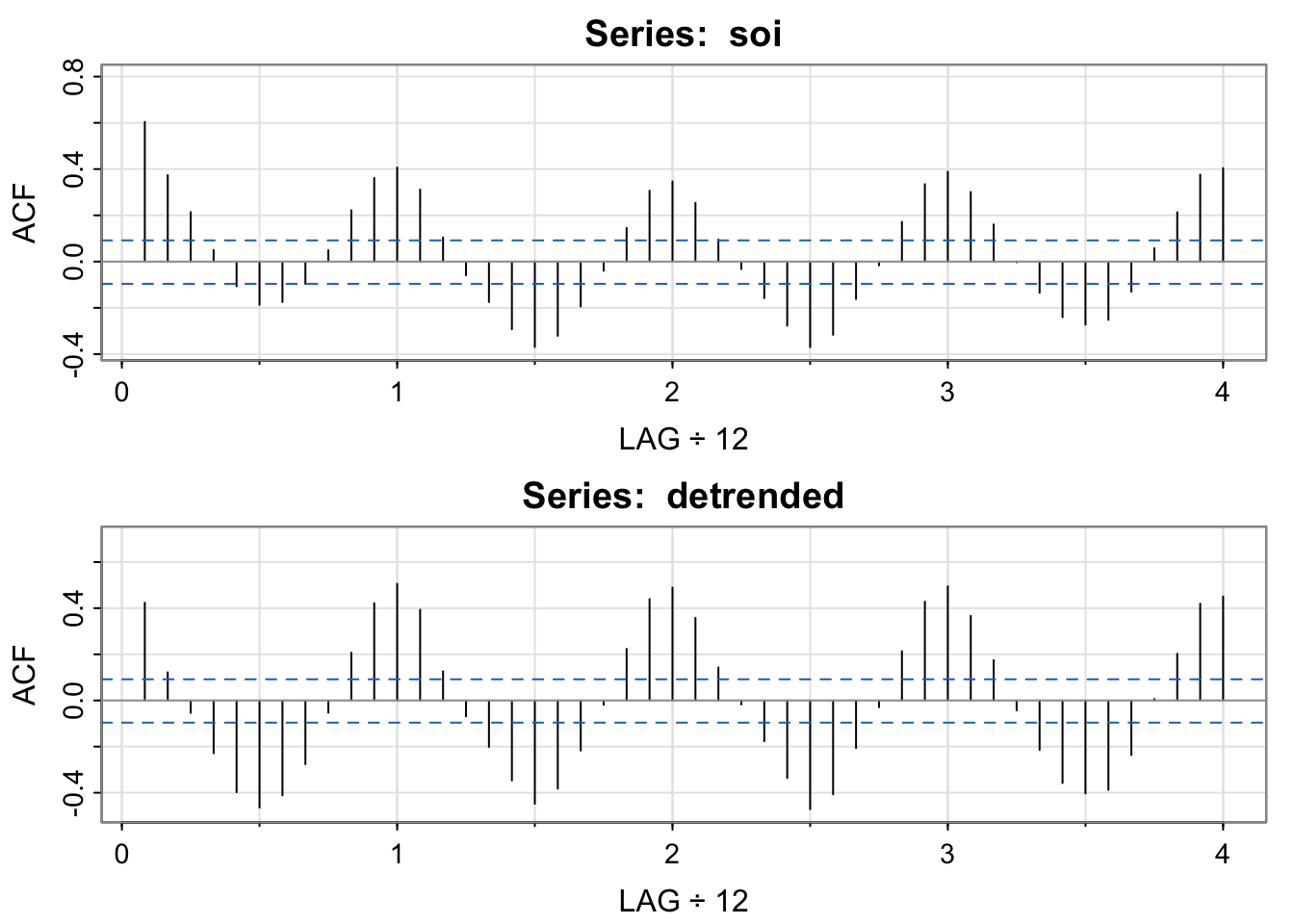

 [1]  0.42  0.12 -0.05 -0.23 -0.40 -0.46 -0.41 -0.28 -0.05  0.21  0.42  0.51
[13]  0.39  0.13 -0.07 -0.20 -0.35 -0.45 -0.38 -0.22 -0.02  0.22  0.44  0.49
[25]  0.36  0.14 -0.02 -0.18 -0.34 -0.47 -0.41 -0.21 -0.03  0.21  0.43  0.49
[37]  0.37  0.17 -0.04 -0.21 -0.36 -0.40 -0.39 -0.24  0.01  0.20  0.42  0.45

1. Describe the trend captured by the kernel smoother. The Kernel smoother appears very similar to the moving average smoother, capturing the longer-term El Niño pattern and smoothing out the annual variation
2. Change the bandwith to 2 and re-plot the kernel smoother and soi series. Repeat with a bandwidth of 0.5. What do you think the bandwidth parameter does? The higher the bandwidth, the “smoother” the kernel.
3. Detrend the soi series with respect to the original kernel smoother with bandwidth 1. Here, we just subtract the estimated trend from the observed series. Note that here we do not have missing values at the ends of the series.
4. Plot the detrended soi series. ** It looks pretty stationary**
5. Plot the acf of the soi series, the kernel smoother trend estimate, and detrended series. What do you notice? Similar to the moving average smoother, we can see the structure as a result of the smoothing in the acf of the kernel smoother. The acf of the original series and the de-trended series look similar. Again, all have temporal structure.

What is a kernel?

A kernel is a moving average smoother that uses a weight function (the kernel) to average the observations: \[ m_t = \sum_{i = 1}^n w_i(t)x_{t_i} \] Where the weight function is

\[ w_i(t) = K \left ( \frac{t-t_i}{b}\right ) / \sum_{k = 1}^n K \left(\frac{t-t_k}{b} \right ) \] Where \(K(z) = \exp(-z^2/2)\) (anyone recognize this?)

How does this compare with the Moving Average smoother?

Interpretation of bandwidth

Since time is in years here, and we would expect yearly cycles, we use a bandwidth of 1 to approximately smooth over the year.

So, bandwidth does control the degree of smoothness, but the actual value depends on the unit of time measurement (years, months, days, etc.)

If the data were monthly, we would use a bandwidth of 12:

SOI = ts(soi, freq = 1) ## convert to monthly
tsplot(SOI) ## note the x-axis
lines(ksmooth(time(SOI), SOI, "normal", bandwidth = 12), lwd = 2, col = 4)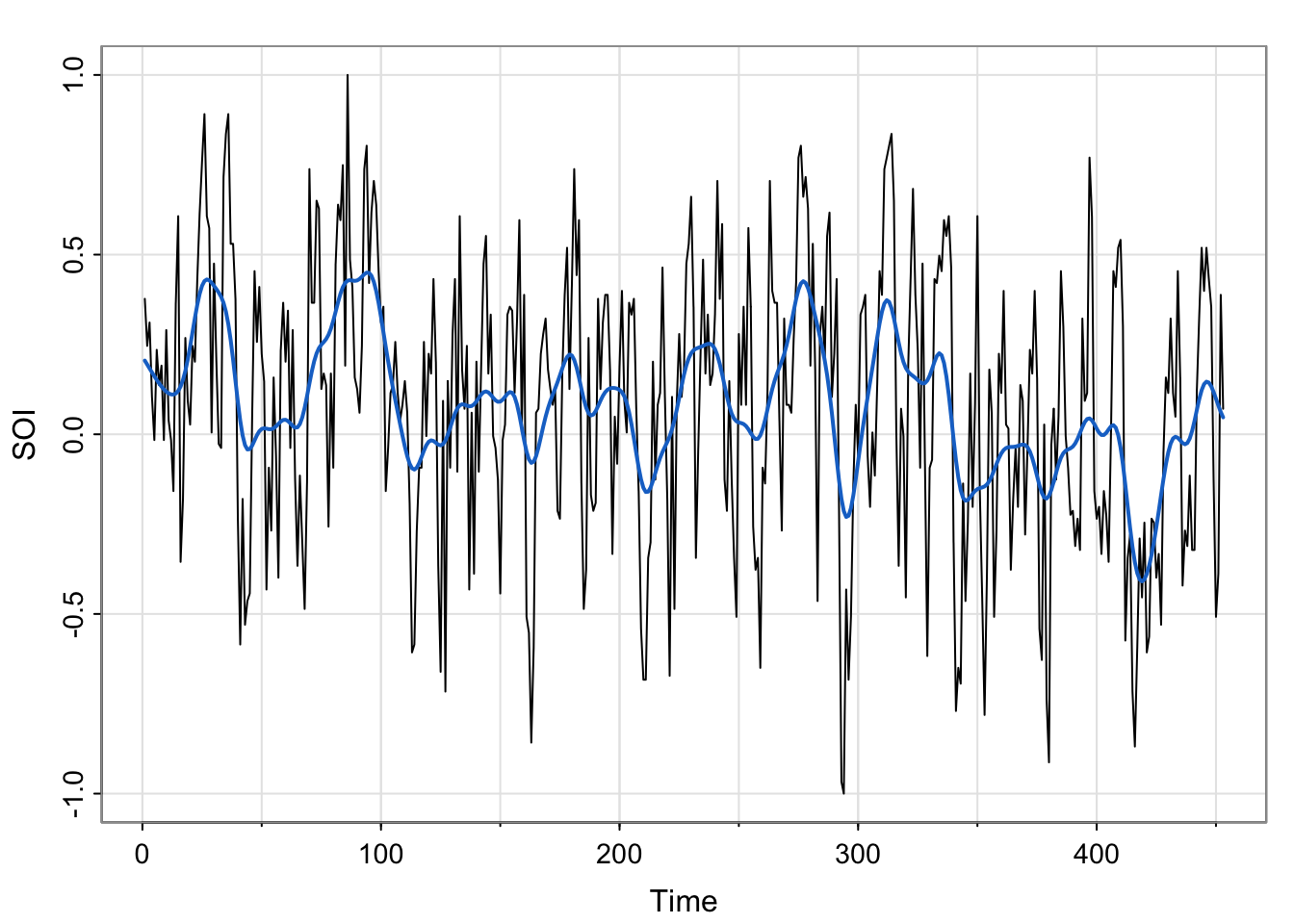

Activity 4: Loess (Example 3.18)

Code source

tsplot(soi, col=astsa.col(4,.6))
lines(lowess(soi, f=.05), lwd=2, col=4) # El Niño cycle
# lines(lowess(soi), lty=2, lwd=2, col=2) # trend (with default span)
#- or -#
##-- trend with CIs using loess --##
lo = predict(loess(soi ~ time(soi)), se=TRUE)
trnd = ts(lo$fit, start=1950, freq=12) # put back ts attributes
lines(trnd, col=6, lwd=2)
 L  = trnd - qt(0.975, lo$df)*lo$se
 U  = trnd + qt(0.975, lo$df)*lo$se
 xx = c(time(soi), rev(time(soi)))
 yy = c(L, rev(U))
polygon(xx, yy, border=8, col=gray(.6, alpha=.4))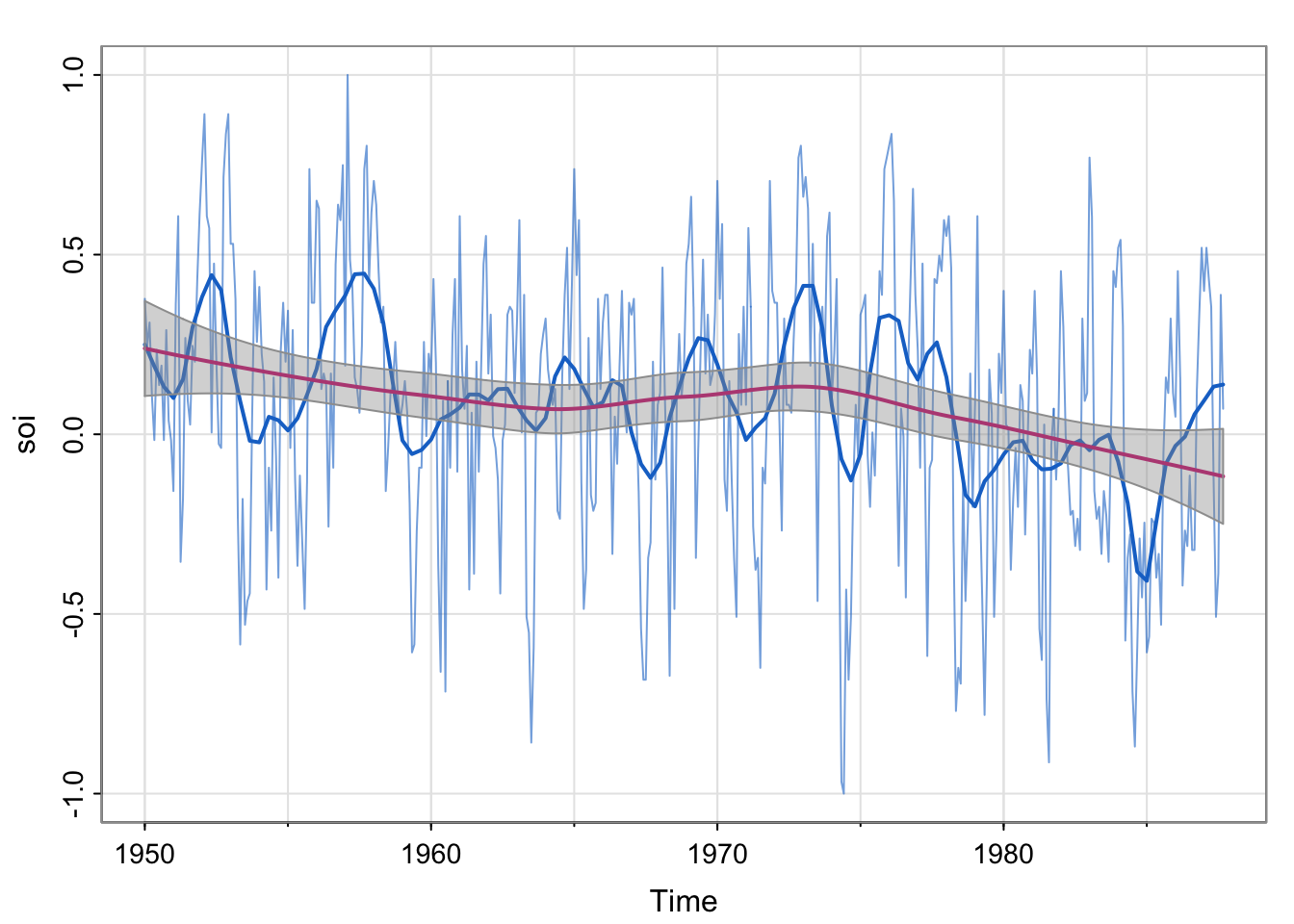

## detrend wrt "linear" trend


## detrend wrt "seasonal" trend 


## detrend wrt both

1. Notice that there are two trends here. Describe the patterns in each.
2. Note that the two smoother estimates use different functions. lowess specifies the f parameter, which is called the bandwidth . What is the name of argument that controls the the span parameter for the function . What does the span parameter control?
3. Detrend the soi series with respect to the linear trend smoother and plot it, then do the same for the El Niño trend, then do the same subtracting off both. How do they look?

Activity 4 Solutions

Code source

tsplot(soi, col=astsa.col(4,.6))
lines(lowess(soi, f=.05), lwd=2, col=4) # El Niño cycle
# lines(lowess(soi), lty=2, lwd=2, col=2) # trend (with default span)
#- or -#
##-- trend with CIs using loess --##
lo = predict(loess(soi ~ time(soi), span = 1), se=TRUE)
trnd = ts(lo$fit, start=1950, freq=12) # put back ts attributes
lines(trnd, col=6, lwd=2)
 L  = trnd - qt(0.975, lo$df)*lo$se
 U  = trnd + qt(0.975, lo$df)*lo$se
 xx = c(time(soi), rev(time(soi)))
 yy = c(L, rev(U))
polygon(xx, yy, border=8, col=gray(.6, alpha=.4))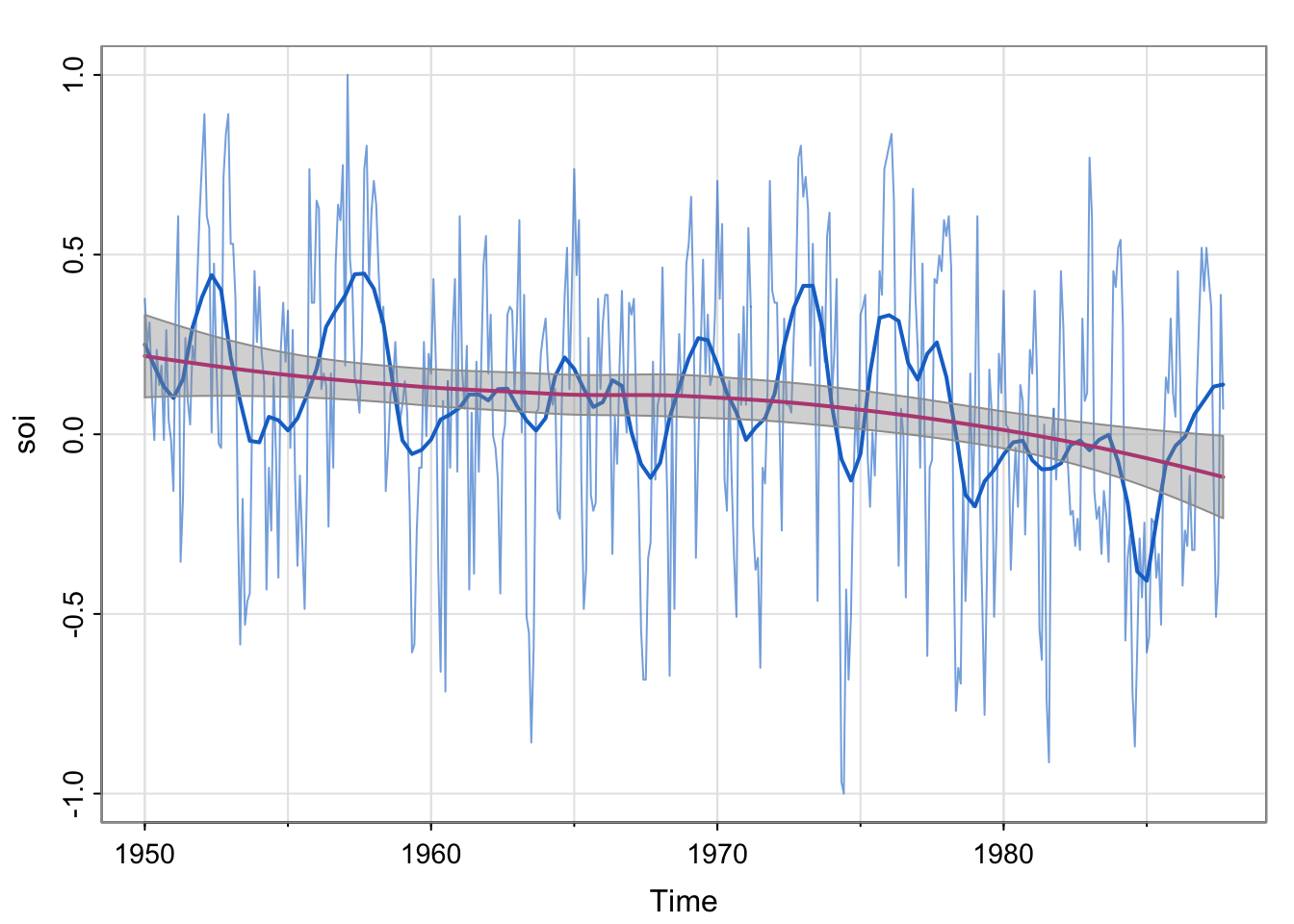

## detrend wrt "linear" trend
tsplot(soi - trnd)

## detrend wrt "seasonal" trend 
smoother <- lowess(soi, f=.05)
tsplot(soi - smoother$y)

## detrend wrt both
tsplot(soi- trnd - smoother$y)

1. Notice that there are two trends here. Describe the patterns in each. There appears to be an approximately linear decreasing trend, and a trend which is similar to the moving average and kernel smoother. The linear-ish trend has a confidence band around it (have we seen that before?)

2. Note that the two smoother estimates use different functions. lowess specifies the f parameter, which is called the bandwidth . What is the name of argument that controls the the span parameter for the function . What does the span parameter control?

Looking at the documentation for loess, we see the function has an argument called span, and the defualt is 0.75. Note that the book is incorrect that the default is 2/3. The span controls the degree of smoothing. We will talk about what that means.

3. Detrend the soi series with respect to the linear trend smoother and plot it, then do the same for the El Niño trend, then do the same subtracting off both. How do they look? They all look fairly similar.

Revisiting the Climate.gov website

More about SOI on Climate.gov

Compare the plot to the smoother estimates we have plotted for the various activities.